题目内容
阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1,y1),B(x2,y2),AB中点P的坐标为(xp,yp).由xp﹣x1=x2﹣xp,得 ,同理
,同理 ,所以AB的中点坐标为
,所以AB的中点坐标为 .由勾股定理得
.由勾股定理得 ,所以A、B两点间的距离公式为
,所以A、B两点间的距离公式为 .
.
注:上述公式对A、B在平面直角坐标系中其它位置也成立.
解答下列问题:
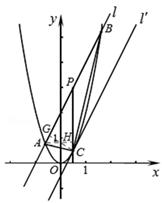
如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
(1)求A、B两点的坐标及C点的坐标;
(2)连结AB、AC,求证△ABC为直角三角形;
(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
解:(1)由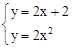 ,解得:
,解得: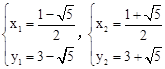 。
。
∴A,B两点的坐标分别为:A(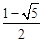 ,
,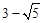 ),B(
),B(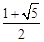 ,
,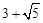 )。
)。
∵P是A,B的中点,由中点坐标公式得P点坐标为(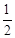 ,3)。
,3)。
又∵PC⊥x轴交抛物线于C点,将x=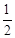 代入y=2x2中得y=
代入y=2x2中得y=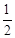 ,
,
∴C点坐标为(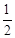 ,
,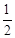 )。
)。
(2)证明:由两点间距离公式得: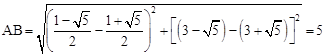 ,
,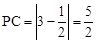 ,
,
∴PC=PA=PB。
∴∠PAC=∠PCA,∠PBC=∠PCB。
∴∠PAC+∠PCB=90°,即∠ACB=90°。∴△ABC为直角三角形。
(3)如图,过点C作CG⊥AB于G,过点A作AH⊥PC于H,
则H点的坐标为(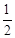 ,
,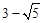 )。
)。
∴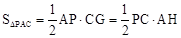 。
。
∴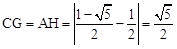 。
。
又直线l与l′之间的距离等于点C到l的距离CG,∴直线l与l′之间的距离为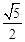 。
。
解析

练习册系列答案
相关题目
某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
| 销售单价x(元/件) | … | 55 | 60 | 70 | 75 | … |
| 一周的销售量y(件) | … | 450 | 400 | 300 | 250 | … |
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的贷款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?

 与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
 A,那么它的表达式可表示为:
A,那么它的表达式可表示为: ]
]
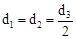 ?若存在,请直接写出d3的值;若不存在,请说明理由.
?若存在,请直接写出d3的值;若不存在,请说明理由.
 过抛物线
过抛物线 的顶点P,如图所示.
的顶点P,如图所示.
 ,抛物线
,抛物线 (a≠0)经过点A(4,0)与点(﹣2,6).
(a≠0)经过点A(4,0)与点(﹣2,6).