题目内容
如图,抛物线y=ax2+bx+c的开口向下,与x轴交于点A(﹣3,0)和点B(1,0).与y轴交于点C,顶点为D.
(1)求顶点D的坐标.(用含a的代数式表示);
(2)若△ACD的面积为3.
①求抛物线的解析式;
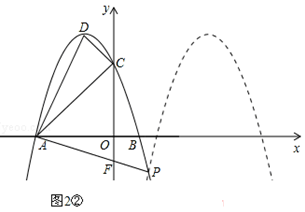
②将抛物线向右平移,使得平移后的抛物线与原抛物线交于点P,且∠PAB=∠DAC,求平移后抛物线的解析式.
解:(1)∵抛物线y=ax2+bx+c与x轴交于点A(﹣3,0)和点B(1,0),
∴抛物线解析式为y=a(x+3)(x﹣1)=ax2+2ax﹣3a。
∵y= ax2+2ax﹣3a =a(x2+2x﹣3)=a(x+1)2﹣4a,
∴顶点D的坐标为(﹣1,﹣4a)。
(2)①如图1,设AC与抛物线对称轴的交点为E,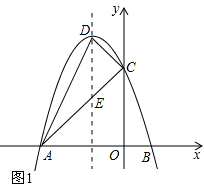
∵抛物线y=ax2+2ax﹣3a与y轴交于点C,
∴C点坐标为(0,﹣3a)。
设直线AC的解析式为:y=kx+t,
则: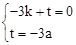 ,解得:
,解得: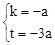 。
。
∴直线AC的解析式为:y=﹣ax﹣3a。
∴点E的坐标为:(﹣1,﹣2a)。∴DE=﹣4a﹣(﹣2a)=﹣2a。
∴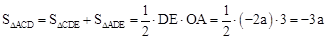 。
。
∴﹣3a=3,解得a=﹣1。
∴抛物线的解析式为y=﹣x2﹣2x+3。
②∵y=﹣x2﹣2x+3,∴顶点D的坐标为(﹣1,4),C(0,3)。
∵A(﹣3,0),
∴AD2=(﹣1+3)2+(4﹣0)2=20,CD2=(﹣1﹣0)2+(4﹣3)2=2,
AC2=(0+3)2+(3﹣0)2=18。
∴AD2=CD2+AC2。∴∠ACD=90°。
∴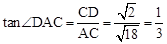 。
。
∵∠PAB=∠DAC,∴tan∠PAB=tan∠DAC=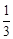 。
。
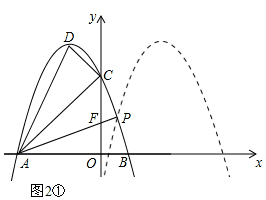
如图2,设y=﹣x2﹣2x+3=﹣(x+1)2+4向右平移后的抛物线解析式为y=﹣(x+m)2+4,两条抛物线交于点P,直线AP与y轴交于点F,
∵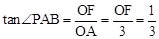 ,
,
∴OF=1,则F点的坐标为(0,1)或(0,﹣1)。
分两种情况:
(Ⅰ)如图2①,当F点的坐标为(0,1)时,易求直线AF的解析式为 ,
,
由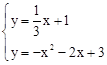 解得,
解得,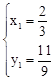 ,
,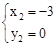 (舍去)。
(舍去)。
∴P点坐标为( ,
,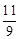 )。
)。
将P点坐标( ,
,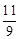 )代入y=﹣(x+m)2+4,
)代入y=﹣(x+m)2+4,
得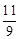 =﹣(
=﹣( +m)2+4,解得m1=
+m)2+4,解得m1=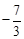 ,m2=1(舍去)。
,m2=1(舍去)。
∴平移后抛物线的解析式为y=﹣(x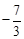 )2+4。
)2+4。
(Ⅱ)如图2②,当F点的坐标为(0,﹣1)时,易求直线AF的解析式为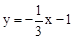 。
。
由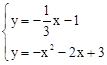 解得,
解得, ,
,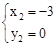 (舍去)。
(舍去)。
∴P点坐标为(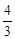 ,
, )。
)。
将P点坐标(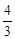 ,
, )代入y=﹣(x+m)2+4,
)代入y=﹣(x+m)2+4,
得 =﹣(
=﹣(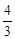 +m)2+4,解得m1=
+m)2+4,解得m1=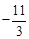 ,m2=1(舍去)。
,m2=1(舍去)。
∴平移后抛物线的解析式为y=﹣(x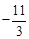 )2+4。
)2+4。
综上可知,平移后抛物线的解析式为y=﹣(x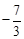 )2+4或y=﹣(x
)2+4或y=﹣(x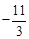 )2+4。
)2+4。
解析试题分析:(1)已知抛物线与x轴的两交点的横坐标分别是﹣3和1,设抛物线解析式的交点式y=a(x+3)(x﹣1),再配方为顶点式,可确定顶点坐标。
(2)①设AC与抛物线对称轴的交点为E,先运用待定系数法求出直线AC的解析式,求出点E的坐标,即可得到DE的长,然后由S△ACD=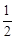 ×DE×OA列出方程,解方程求出a的值,即可确定抛物线的解析式。
×DE×OA列出方程,解方程求出a的值,即可确定抛物线的解析式。
②先运用勾股定理的逆定理判断出在△ACD中∠ACD=90°,利用三角函数求出tan∠DAC=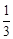 。设抛物线向右平移后的抛物线解析式为y=﹣(x+m)2+4,两条抛物线交于点P,直线AP与y轴交于点F.根据正切函数的定义求出OF=1。分两种情况进行讨论:(Ⅰ)如图2①,F点的坐标为(0,1),(Ⅱ)如图2②,F点的坐标为(0,﹣1).针对这两种情况,都可以先求出点P的坐标,再得出m的值,进而求出平移后抛物线的解析式。
。设抛物线向右平移后的抛物线解析式为y=﹣(x+m)2+4,两条抛物线交于点P,直线AP与y轴交于点F.根据正切函数的定义求出OF=1。分两种情况进行讨论:(Ⅰ)如图2①,F点的坐标为(0,1),(Ⅱ)如图2②,F点的坐标为(0,﹣1).针对这两种情况,都可以先求出点P的坐标,再得出m的值,进而求出平移后抛物线的解析式。

某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
| 销售单价x(元/件) | … | 55 | 60 | 70 | 75 | … |
| 一周的销售量y(件) | … | 450 | 400 | 300 | 250 | … |
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的贷款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?
(2013年浙江义乌10分)为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数.下表提供了部分采购数据.
| 采购数量(件) | 1 | 2 | … |
| A产品单价(元/件) | 1480 | 1460 | … |
| B产品单价(元/件) | 1290 | 1280 | … |
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的
 ,且A产品采购单价不低于1200元.求该商家共有几种进货方案;
,且A产品采购单价不低于1200元.求该商家共有几种进货方案;(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完.在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.

 过抛物线
过抛物线 的顶点P,如图所示.
的顶点P,如图所示.

 与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
 ,抛物线
,抛物线 (a≠0)经过点A(4,0)与点(﹣2,6).
(a≠0)经过点A(4,0)与点(﹣2,6).
 (
( )与y轴交于点A,其对称轴与x轴交于点B。
)与y轴交于点A,其对称轴与x轴交于点B。
 这一段位于直线l的上方,并且在
这一段位于直线l的上方,并且在 这一段位于直线AB的下方,求该抛物线的解析式。
这一段位于直线AB的下方,求该抛物线的解析式。