题目内容
如图,反比例函数y=
(k<0)的图象经过点A(-
,m),过A作AB⊥x轴于点B,△AOB的面积为
.?
(1)求k和m的值;?
(2)若过A点的直线y=ax+b与x轴交于C点,且∠ACO=30°,求此直线的解析式.

| k |
| x |
| 3 |
| 3 |
(1)求k和m的值;?
(2)若过A点的直线y=ax+b与x轴交于C点,且∠ACO=30°,求此直线的解析式.

(1)S△AOB=
•OB•AB=
×
•m=
∴m=2,A(-
,2)
∵反比例函数y=
(k<0)的图象经过点A
∴k=-2
;
(2)分类讨论:
①C点在负半轴.在△ABC中,AB=2,∠C=30°,
∴BC=2
,C(-3
,0);
解方程组
得
,
所以直线解析式为y=
x+3.
②C点在正半轴.在△ABC中,AB=2,∠C=30°,
∴BC=2
,C(
,0);
解方程组
得,
,
所以满足条件的直线解析式为y=-
x+1.
综上所述,所以满足条件的直线解析式为y=
x+3和y=-
x+1.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴m=2,A(-
| 3 |
∵反比例函数y=
| k |
| x |
∴k=-2
| 3 |
(2)分类讨论:
①C点在负半轴.在△ABC中,AB=2,∠C=30°,

∴BC=2
| 3 |
| 3 |
解方程组
|
|
所以直线解析式为y=
| ||
| 3 |
②C点在正半轴.在△ABC中,AB=2,∠C=30°,
∴BC=2
| 3 |
| 3 |
解方程组
|
|
所以满足条件的直线解析式为y=-
| ||
| 3 |
综上所述,所以满足条件的直线解析式为y=
| ||
| 3 |
| ||
| 3 |

练习册系列答案
相关题目


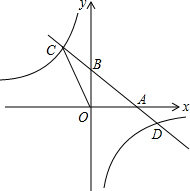 A=3,点C的横坐标为-3,tan∠BAO=
A=3,点C的横坐标为-3,tan∠BAO=
 向银行付款y万元,预计x年后结清余款,y与x的函数关系如下图所示,试根据图象所提供的信息,回答下列问题:
向银行付款y万元,预计x年后结清余款,y与x的函数关系如下图所示,试根据图象所提供的信息,回答下列问题:



 D两点.
D两点.