Question

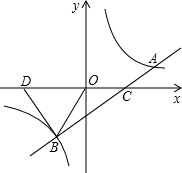
如图，直线y=2x与双曲线y=

8

x

交于点A、E，直线AB交双曲线于另一点B（2m，m），连接EB并延长交x轴于点F．
（1）m=______；
（2）求直线AB的解析式；
（3）求△EOF的面积；
（4）若点P为坐标平面内一点，且以A，B，E，P为顶点的四边形是平行四边形，请直接写出所有满足条件的点P的坐标．

Answer 1

（1）∵点B（2m，m）在双曲线y=

8

x

上，
∴2m•m=8，解得m=±2，而m＞0，
∴m=2．
故答案为2；

（2）m=2，则B点坐标为（4，2），
解方程组

y=2x y= 8 x

得

x=-2 y=-4

或

x=2 y=4

，
∴A点坐标为（-2，-4），E点坐标为（2，4），
设直线AB的解析式为y=kx+b，
把A（-2，-4），B（4，2）代入得：-2k+b=-4，4k+b=2，解方程组得k=1，b=-2，
∴直线AB的解析式为y=x-2；

（3）设直线EB的解析式为y=kx+b，
把E（2，4），B（4，2）代入得：2k+b=4，4k+b=2，解方程组得k=-1，b=6，
∴直线EB的解析式为y=-x+6，
令y=0，则-x+6=0，得x=6，即F点的坐标为（6，0），
∴△EOF的面积=

1

2

×6×4=12；

（4）满足条件的点P的坐标为（-4，-2）、（0，-6）、（8，10）．