题目内容
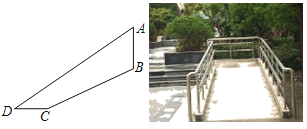
【题目】在商场里，为方便一部分残疾人出入，商场特意设计了一种特殊通道“无障碍通道”，如图，线段BC表示无障碍通道，线段AD表示普通扶梯，其中“无障碍通道”BC的坡度（或坡比）为i＝1：2，BC＝12
米，CD＝6米，∠D＝30°，（其中点A、B、C、D均在同一平面内）则垂直升降电梯AB的高度约为（ ）米．
A.10
B.10﹣12C.12D.10+12
【答案】B
【解析】
根据勾股定理，可得CE，BE的长，根据正切函数，可得AE的长，再根据线段的和差，可得答案．
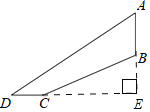
解：如图，延长AB交DC的延长线于点E，
，
由BC的坡度（或坡比）为i＝1：2，得BE：CE＝1：2．
设BE＝x，CE＝2x．
在Rt△BCE中，由勾股定理，得BE2+CE2＝BC2，
即x2+（2x）2＝（12
）2，
解得x＝12（米），
∴BE＝12（米），CE＝24（米），
DE＝DC+CE＝6+24＝30（米），
由tan30°＝
，得
，
解得AE＝10
．
由线段的和差，得
AB＝AE﹣BE＝（10﹣12）（米），
故选：B．
练习册系列答案
相关题目
