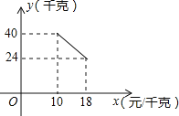
题目内容
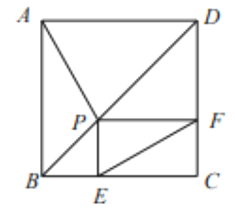
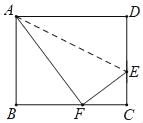
【题目】折叠矩形ABCD,使点D落在BC边上的点F处.

(1)求证:△ABF∽△FCE;
(2)若DC=8,CF=4,求矩形ABCD的面积S.
【答案】(1)证明见解析;(2)80.
【解析】
(1)根据矩形性质和折叠性质证△ABF∽△FCE;(2)在Rt△EFC中,EF2=CE2+CF2,求DE=EF,根据相似三角形性质,求AD=AF=10,S=ADCD.
(1)∵矩形ABCD中,
∠B=∠C=∠D=90°.
∴∠BAF+∠AFB=90°.
由折叠性质,得∠AFE=∠D=90°.
∴∠AFB+∠EFC=90°.
∴∠BAF=∠EFC.
∴△ABF∽△FCE;
(2)由折叠性质,得AF=AD,DE=EF.
设DE=EF=x,则CE=CD﹣DE=8﹣x,
在Rt△EFC中,EF2=CE2+CF2,
∴x2=(8﹣x)2+42.
解得x=5.
由(1)得△ABF∽△FCE,
![]()
![]()
∴AD=AF=10.
∴S=ADCD=10×8=80.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目