ƒøƒĞ»ı
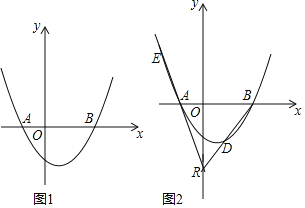
°æƒø°ø“—÷™≈◊ŒÔœşy£Ωa£®x2£≠cx£≠2c2£©£®a£æ0£©Ωªx÷·”ĞA°¢B¡Ωµ„£®µ„A‘е„Bµƒ◊Û≤‡£©£¨Ωªy÷·”е„C£Æ
£®1£© »°A£®£≠1£¨0£©£¨‘Úµ„Bµƒ◊¯±ÍŒ™___________£ª
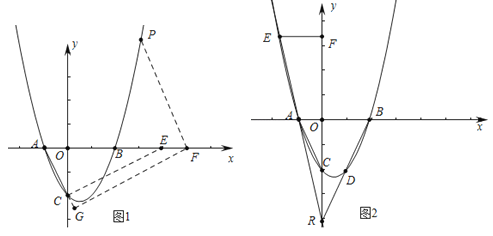
£®2£© »ÙA£®£≠1£¨0£©£¨a£Ω1£¨µ„PŒ™µĞ“ªœÛœŞµƒ≈◊ŒÔœş£¨“‘PŒ™‘≤–ƒ£¨![]() Œ™∞Îæ∂µƒ‘≤«°∫√”ÎACœ‡«–£¨«ÛPµ„◊¯±Í£ª
Œ™∞Îæ∂µƒ‘≤«°∫√”ÎACœ‡«–£¨«ÛPµ„◊¯±Í£ª
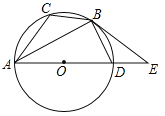
£®3£© »ÁÕº£¨µ„R£®0£¨n£©‘Ğy÷·∏∫∞Î÷·…œ£¨÷±œşRBΩª≈◊ŒÔœş”Ğ¡Ì“ªµ„D£¨÷±œşRAΩª≈◊ŒÔœş”ĞE£Æ»ÙDR£ΩDB£¨EF°Õy÷·”ĞF£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
°æ¥∞∏°ø(1) B(2£¨0)(2) P(3£¨4)(3) ![]()
°æΩ‚Œˆ°ø£®1£©Ω´Aµƒ◊¯±Í¥˙»Î£¨«Û≥ˆcº¥ø…µ√≥ˆµ„Bµƒ◊¯±Í£¨∞—a£¨c¥˙»Îµ„Cµƒ◊¯±Íº¥ø…£ª
£®2£©»ÁÕº1÷–£¨◊˜CE°ÕACΩªx÷·”ĞE£¨‘Ğx÷·…œ»°“ªµ„F£¨◊˜FG°ÕAC”ĞG£¨◊˜FP°ŒAC£Æµ±FG=![]() ±£¨µ„PµΩ÷±œşACµƒæ‡¿Î“≤ «
±£¨µ„PµΩ÷±œşACµƒæ‡¿Î“≤ «![]() £¨¥À ±“‘PŒ™‘≤–ƒ
£¨¥À ±“‘PŒ™‘≤–ƒ![]() Œ™∞Îæ∂µƒ‘≤«°∫√”ÎACœ‡«–£¨œÎ∞Ï∑®«Û≥ˆ÷±œşPFµƒΩ‚Œˆ Ω£¨¿˚”√∑Ω≥Ã◊È«ÛΩªµ„Pµƒ÷µ◊¯±Íº¥ø…£Æ
Œ™∞Îæ∂µƒ‘≤«°∫√”ÎACœ‡«–£¨œÎ∞Ï∑®«Û≥ˆ÷±œşPFµƒΩ‚Œˆ Ω£¨¿˚”√∑Ω≥Ã◊È«ÛΩªµ„Pµƒ÷µ◊¯±Íº¥ø…£Æ
£®3£©¿˚”√DR=DBµ√≥ˆµ„Dµƒ◊¯±Í£¨∂¯µ„D‘Ğ≈◊ŒÔœş…œ£¨º¥ø…µ√≥ˆRµƒ◊¯±Í£¨Ω¯∂¯«Û≥ˆ÷±œşARµƒΩ‚Œˆ Ωº¥ø…µ√≥ˆµ„Eµƒ◊¯±Í£¨«Û≥ˆEF°¢ABº¥ø…Ω‚æˆŒ £Æ
£®1£©°ş≈◊ŒÔœşy=a£®x2©Åcx©Å2c2£©=a£®x+c£©£®x©Å2c£©£¨°‡A£®©Åc£¨0£©£¨B£®2c£¨0£©£¨C£®0£¨©Å2ac2£©£¨µ±A£®©Å1£¨0£© ±£¨°‡©Åc=©Å1£¨°‡c=1£¨°‡2c=2£¨°‡B£®2£¨0£©£Æ
π ¥∞∏Œ™£∫£®2£¨0£©£Æ
£®2£©°şa=1£¨c=1£¨°‡B£®2£¨0£©£¨C£®0£¨©Å2£©£¨°‡≈◊ŒÔœşµƒΩ‚Œˆ ΩŒ™y=x2©Åx©Å2£Æ
»ÁÕº1÷–£¨◊˜CE°ÕACΩªx÷·”ĞE£¨‘Ğx÷·…œ»°“ªµ„F£¨◊˜FG°ÕAC”ĞG£¨◊˜FP°ŒAC£Æ
µ±FG=![]() ±£¨µ„PµΩ÷±œşACµƒæ‡¿Î“≤ «
±£¨µ„PµΩ÷±œşACµƒæ‡¿Î“≤ «![]() £¨¥À ±“‘PŒ™‘≤–ƒ
£¨¥À ±“‘PŒ™‘≤–ƒ![]() Œ™∞Îæ∂µƒ‘≤«°∫√”ÎACœ‡«–£Æ
Œ™∞Îæ∂µƒ‘≤«°∫√”ÎACœ‡«–£Æ
°ş°œOAC=°œCAE£¨°œAOC=°œACE=90°„£¨°‡°˜AOC°◊°˜ACE£¨°‡![]() =
=![]() =
=![]() =
=![]() =
=![]() £¨°‡AE=5£¨EC=
£¨°‡AE=5£¨EC=![]() £Æ
£Æ
°şEC°ŒFG£¨°‡![]() =
=![]() =
=![]() £¨°‡AF=6£¨°‡F£®5£¨0£©£Æ
£¨°‡AF=6£¨°‡F£®5£¨0£©£Æ
°ş÷±œşACµƒΩ‚Œˆ ΩŒ™y=©Å2x©Å2£¨…Ë÷±œşPFµƒΩ‚Œˆ ΩŒ™y=©Å2x+b£¨∞—£®5£¨0£©¥˙»Îµ√b=10£¨°‡÷±œşPFµƒΩ‚Œˆ ΩŒ™y=©Å2x+10£¨”…![]() £¨Ω‚µ√£∫
£¨Ω‚µ√£∫![]() ªÚ
ªÚ![]() £Æ
£Æ
°şµ„P‘еГªœÛœŞ£¨°‡P£®3£¨4£©£Æ
£®3£©»ÁÕº2÷–£¨°şDR=DB£¨R£®0£¨n£©£¨B£®2c£¨0£©£¨°‡D£®c£¨![]() n£©£Æ
n£©£Æ
°şµ„D‘Ğ≈◊ŒÔœşy=a£®x2©Åcx©Å2c2£©…œ£¨°‡a£®c2©Åc2©Å2c2£©=![]() n£¨°‡n=©Å4ac2£¨°‡R£®0£¨©Å4ac2£©£Æ
n£¨°‡n=©Å4ac2£¨°‡R£®0£¨©Å4ac2£©£Æ
°şA£®©Åc£¨0£©£¨°‡÷±œşARµƒΩ‚Œˆ ΩŒ™y=©Å4acx©Å4ac2¢Ÿ£Æ
°şµ„E‘Ğ≈◊ŒÔœşy=a£®x+c£©£®x©Å2c£©¢Ğ…œ£¨¡™¡¢¢Ÿ¢Ğµ√£∫E£®©Å2c£¨©Å12ac2£©£¨°‡EF=2c£¨AB=3c£¨°‡![]() =
=![]() £Æ
£Æ