题目内容
【题目】在四边形ABCD中,点E是对角线BD上一点,点Q是AD边上一点,BQ交AE于点P,∠ABQ=∠DAE,点F是AB边的中点.
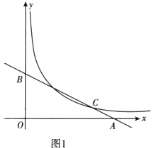
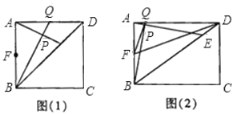
(1)当四边形ABCD是正方形时,如图(1).
①若BE=BA,求证:△ABP≌△EBP;
②若BE=4DE,求证:AF2=AQ·AD.
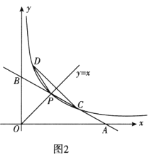
(2)当四边形ABCD是矩形时,如图(2),连接FQ,FD.若BE=4DE,求证:∠AFQ=∠ADF.
【答案】(1)①证明见解析;②证明见解析;(2)证明见解析.
【解析】
(1)①由HL可证明Rt△ABP![]() Rt△EBP;
Rt△EBP;
②证明:过点E作EG⊥AD于点G可得△DEG∽△DBA,可得![]() ,以及△BAQ∽△AGE,可得
,以及△BAQ∽△AGE,可得![]() ,设DG=a,则GE=a,DA=5a,AB=5a,AG=4a.AQ=
,设DG=a,则GE=a,DA=5a,AB=5a,AG=4a.AQ=![]() ,代入即可证明:AF2=AQ·AD;
,代入即可证明:AF2=AQ·AD;
(2)延长AE交于CD边于点H,设DH=m,由AB∥CD,可得△DEH∽△BEA,可得AF=2m,由△BAQ∽△ADH,可得![]() 即AQ·DA=DH·AB=4m2=AF2,可证△AFQ∽△ADF,即可得出∠AFO=∠ADF.
即AQ·DA=DH·AB=4m2=AF2,可证△AFQ∽△ADF,即可得出∠AFO=∠ADF.
(1)①证明:在正方形ABCD中,∠ABQ=∠DAE.
∵∠ABQ+∠BAP=∠DAE+∠BAP=∠BAD=90°,
∴∠BPA=∠BPE=90°.
在Rt△ABP和Rt△EBP中,
![]() ,
,
∴Rt△ABP![]() Rt△EBP
Rt△EBP
②证明:过点E作EG⊥AD于点G,如图
∴∠GED=∠BAD=90°
∵∠GDE=∠ADB
∴△DEG∽△DBA,
∴![]()
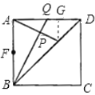
设DG=a,则GE=a,
∴DA=5a,AB=5a,AG=4a.
∵∠ABQ=∠DAE,∠BAQ=∠AGE,
∴△BAQ∽△AGE,
∴![]()
即AQ=![]()
∵F是AB边的中点,
∴![]()
又∵AQ·AD=![]() ,
,
∴AF2=AQ·AD
(2)证明:延长AE交于CD边于点H,设DH=m
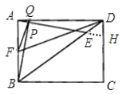
∵四边形ABCD是矩形,
∴AB∥CD,
∴△DEH∽△BEA,
∴![]() 即AB=4m,
即AB=4m,
∴AF=2m
∵∠BAQ=∠APB=90°
∴∠ABQ+∠BAP=∠DAH+∠BAP=90°
∴∠ABQ=∠DAH
∵∠BAQ=∠ADH=90°,∠ABQ=∠DAH
∴△BAQ∽△ADH,,
∴![]() 即AQ·DA=DH·AB=4m2=AF2,
即AQ·DA=DH·AB=4m2=AF2,
∴![]()
又∠FAO=∠DAF,
∴△AFQ∽△ADF,
∴∠AFO=∠ADF.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案