Question

【题目】△ABC中，BC=10，AB=，∠ABC=30°，点P在直线AC上，点P到直线AB的距离为1，则CP的长为_____．

Answer 1

【答案】或 ．

【解析】分析：过点C作CD⊥AB交BA的延长线于点D，根据∠ABC的正弦和余弦可以求出CD、BD的长度，从而可以求出AD的长度，然后利用勾股定理即可求出AC的长度，再利用相似三角形对应边成比例列式求出AP的长度，再分点P在线段AC上与点P在射线CA上两种情况讨论求解．

详解：如图，过点C作CD⊥AB交BA的延长线于点D，

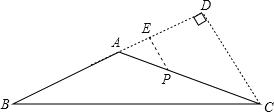
∵BC=10，∠ABC=30°，

∴CD=BCsin30°=5，

BD=BCcos30°=5，

∵AB=4，

∴AD=BD-AB=5-4=，

在Rt△ACD中，AC==．

过P作PE⊥AB，与BA的延长线于点E，

∵点P在直线AC上，点P到直线AB的距离为1，

∴△APE∽△ACD，

∴，

即，

解得AP=，

∴①点P在线段AC上时，CP=AC-AP=2-=，

②点P在射线CA上时，CP=AC+AP=2+=．

综上所述，CP的长为或．

故答案为：或．