��Ŀ����
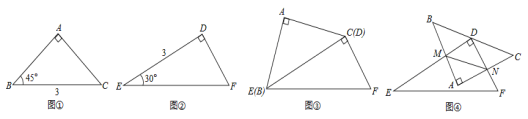
����Ŀ����ͼ���ڵȱ�������ABC�У���D��E�ֱ��ڱ�AB��AC�ϣ�AD=AE������BE��CD����M��N��P�ֱ���BE��CD��BC���е㣬����DE��PM��PN��MN��
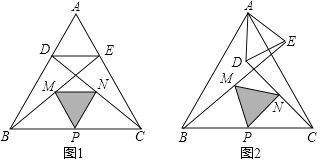
��1���۲���룬��ͼ����PMN��_______�������������ε����ƣ�
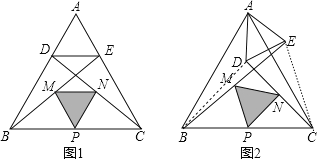
��2��̽��֤������ͼ����ADE�Ƶ�A����ʱ�뷽����ת������PMN����״�Ƿ����ı䣿������ͼ˵�����ɣ�
��3����չ���죬����ADE�Ƶ�A��ƽ����������ת��AD=2��AB=6����ֱ��д����PMN���ܳ������ֵ��
���𰸡���1���ȱ������Σ���2��![]() ����״�������ı䣬��Ϊ�ȱ������Σ����ɼ���������3��
����״�������ı䣬��Ϊ�ȱ������Σ����ɼ���������3��![]() ���ܳ������ֵΪ12
���ܳ������ֵΪ12
��������
��1����ͼ1���ȸ��ݵȱ������ε����ʵõ�AB=AC����ABC=��ACB=60������BD=CE���ٸ�����������λ�����ʵ�PM��CE��PM![]() CE��PN��AD��PN
CE��PN��AD��PN![]() BD���Ӷ��õ�PM=PN����MPN=60�����Ӷ����ж���PMNΪ�ȱ������Σ�
BD���Ӷ��õ�PM=PN����MPN=60�����Ӷ����ж���PMNΪ�ȱ������Σ�
��2������CE��BD����ͼ2���ȸ�����ת�����ʵõ���ABD����ACE����BD=CE����ABD=��ACE��Ȼ��ɵ�PM=PN�������MPN=60�������ǿ��ж���PMNΪ�ȱ������Σ�
��3������AB��AD��BD��AB+AD�����ҽ�����B��A��D����ʱȡ�Ⱥţ��õ�BD�����ֵΪ8����PN�����ֵΪ4��Ȼ���ȷ����PMN���ܳ������ֵ��
��1���ȱ������Σ��������£�
��ͼ1��
�ߡ�ABCΪ�ȱ������Σ���AB=AC����ABC=��ACB=60����
��AD=AE����BD=CE��
�ߵ�M��N��P�ֱ���BE��CD��BC���е㣬��PM��CE��PM![]() CE��PN��AD��PN
CE��PN��AD��PN![]() BD����PM=PN����BPM=��BCA=60������CPN=��CBA=60�������MPN=60�������PMNΪ�ȱ������Σ�
BD����PM=PN����BPM=��BCA=60������CPN=��CBA=60�������MPN=60�������PMNΪ�ȱ������Σ�
�ʴ�Ϊ���ȱ������Σ�
��2����PMN����״�������ı䣬��Ϊ�ȱ������Σ��������£�
����BD��CE������ת�ɵá�BAD=��CAE��
����ABC�ǵȱ������Σ���AB=AC����ACB=��ABC=60����
�֡�AD=AE������ABD����ACE����BD=CE����ABD=��ACE��
��M��BE���е㣬P��BC���е㣬��PM����BCE����λ�ߣ���PM=![]() CE��PM//CE��
CE��PM//CE��
ͬ����֤PN=![]() BD��PN//BD����PM=PN����MPB=��ECB����NPC=��DBC
BD��PN//BD����PM=PN����MPB=��ECB����NPC=��DBC
���MPB+��NPC=��ECB+��DBC=����ACB+��ACE��+����ABC-��ABD��
=��ACB+��ABC=120�������MPN=60��������PMN�ǵȱ������Σ�
��3����PN![]() BD���൱BD��ֵ���ʱ��PN��ֵ���
BD���൱BD��ֵ���ʱ��PN��ֵ���
��AB��AD��BD��AB+AD�����ҽ�����B��A��D����ʱȡ�Ⱥţ�
��BD�����ֵΪ2+6=8����PN�����ֵΪ4�����PMN���ܳ������ֵΪ12��

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�