题目内容
【题目】(2013年广东梅州11分)用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:
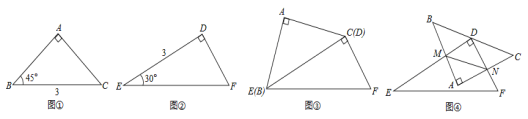
探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.
(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;
(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.
探究二:如图④,将△DEF的顶点D放在△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.
【答案】解:探究一:
(1)依题意画出图形,如答图1所示:
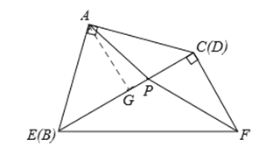
由题意,得∠CFB=60°,FP为角平分线,
则∠CFP=30°。
∴CF=BCsin30°=3×![]() =
=![]() 。
。
∴CP=CFtan∠CFP=![]() ×
×![]() =1。
=1。
过点A作AG⊥BC于点G,则AG=![]() BC=
BC=![]() ,
,
∴PG=CG﹣CP=![]() ﹣1=
﹣1=![]() 。
。
在Rt△APG中,由勾股定理得: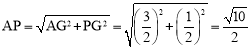 。
。
(2)由(1)可知,FC=![]()
![]() .
.
如答图2所示,以点A为圆心,以FC=![]() 长为半径画弧,与BC交于点P1、P2,则AP1=AP2=
长为半径画弧,与BC交于点P1、P2,则AP1=AP2=![]() 。
。
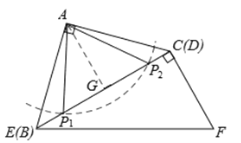
过点A过AG⊥BC于点G,则AG=![]() BC=
BC=![]() ,
,
在Rt△AGP1中,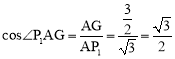 ,∴∠P1AG=30°。
,∴∠P1AG=30°。
∴∠P1AB=45°﹣30°=15°。
同理求得,∠P2AG=30°,∠P2AB=45°+30°=75°。
∴∠PAB的度数为15°或75°。
探究二:△AMN的周长存在有最小值。
如答图3所示,连接AD,
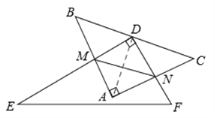
图3
∵△ABC为等腰直角三角形,点D为斜边BC的中点,
∴AD=CD,∠C=∠MAD=45°。
∵∠EDF=90°,∠ADC=90°,∴∠MDA=∠NDC。
∵在△AMD与△CND中,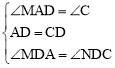 ,
,
∴△AMD≌△CND(ASA)。∴AM=CN。
设AM=x,则CN=x,![]() ,
,
在Rt△AMN中,由勾股定理得:
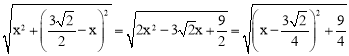 ,
,
∴△AMN的周长为:AM+AN+MN= 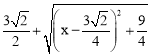 。
。
当x=![]() 时,有最小值,最小值为
时,有最小值,最小值为![]() 。
。
∴△AMN周长的最小值为![]() 。
。
【解析】探究一:(1)如答图1所示,过点A作AG⊥BC于点G,构造Rt△APG,利用勾股定理求出AP的长度。
(2)如答图2所示,符合条件的点P有两个.解直角三角形,利用特殊角的三角函数值求出角的度数。
探究二:如答图3所示,证明△AMD≌△CND,得AM=CN,则△AMN两直角边长度之和为定值;设AM=x,求出斜边MN的表达式,利用二次函数的性质求出MN的最小值,从而得到△AMN周长的最小值。

【题目】某区2014教师招聘有拉开序幕,这给很多有志于教育事业的人员很多机会.下面是今年报考人数统计表(数学)
招聘岗位 | 招聘计划 | 报考人数 | |||
高中教师1 | 研究生 | 高中 | 数学 | 10 | |
高中教师2 | 普通 | 高中 | 数学 | 19 | |
初中教师 | 普通 | 初中 | 数学 | 12 | 55 |
小学教师1 | 普通 | 城区与八镇 | 数学 | 18 | 83 |
小学教师2 | 普通 | 其他 | 数学 | 21 | 93 |
(1)根据上表信息,请制作补完下面的扇形统计图和上述表格.
(2)录取比例最小的是多少?最大的是多少?
(3)如果是你(本科毕业),仅从录取比例上看,你会选择报考哪个岗位?

【题目】某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量频数表
组别(kg) | 频数 |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
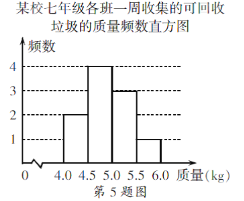
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.
【题目】某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20![]() 时,按2元/
时,按2元/![]() 计费;月用水量超过20
计费;月用水量超过20![]() 时,其中的20
时,其中的20![]() 仍按2元/
仍按2元/![]() 收费,超过部分按
收费,超过部分按![]() 元/
元/![]() 计费.设每户家庭用用水量为
计费.设每户家庭用用水量为![]() 时,应交水费
时,应交水费![]() 元.
元.
(1)分别求出![]() 和
和![]() 时
时![]() 与
与![]() 的函数表达式;
的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
月份 | 四月份 | 五月份 | 六月份 |
交费金额 | 30元 | 34元 | 42.6元 |
小明家这个季度共用水多少立方米?