题目内容
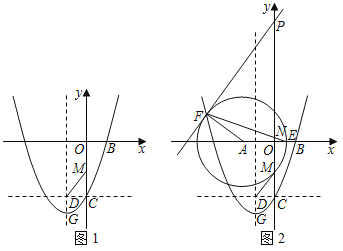
【题目】如图1,经过点B(1,0)的抛物线![]() 与y轴交于点C,其顶点为点G,过点C作y轴的垂线交抛物线对称轴于点D,线段CO上有一动点M,连接DM、DG.
与y轴交于点C,其顶点为点G,过点C作y轴的垂线交抛物线对称轴于点D,线段CO上有一动点M,连接DM、DG.
(1)求抛物线的表达式;
(2)求![]() 的最小值以及相应的点M的坐标;
的最小值以及相应的点M的坐标;
(3)如图2,在(2)的条件下,以点A(﹣2,0)为圆心,以AM长为半径作圆交x轴正半轴于点E.在y轴正半轴上有一动点P,直线PF与⊙A相切于点F,连接EF交y轴于点N,当PF∥BM时,求PN的长.
【答案】(1)![]() ;(2)最小值
;(2)最小值![]() ,M(0,
,M(0,![]() );(3)
);(3)![]() .
.
【解析】
(1)将点B的坐标代入解析式即可求出a的值,即可确定函数解析式;
(2)过点O作直线l与x轴夹角为α,且![]() ,α=45°,过点M作MH⊥直线l于H,推出
,α=45°,过点M作MH⊥直线l于H,推出![]() ,则当D、M、H共线时,
,则当D、M、H共线时,![]() 的值最小,最后求出DH的长即可解答;
的值最小,最后求出DH的长即可解答;
(3)连接BM,延长FA交y轴于J.想办法求出FJ,根据tan∠FPJ=tan∠OMB,可得![]() =
=![]() ,由此构建方程求出PF,再证明PN=PF即可解决问题.
,由此构建方程求出PF,再证明PN=PF即可解决问题.
解:(1)∵抛物线![]() ,经过点B(1,0),
,经过点B(1,0),
∴0=4a﹣![]() ,
,
∴a=![]()
∴![]() .
.
(2)如图1:过点O作直线l与x轴夹角为α,且![]() ,α=45°,过点M作MH⊥直线l于H,
,α=45°,过点M作MH⊥直线l于H,
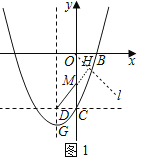
则有![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当D,M,H共线时,![]() 的值最小,
的值最小,
∵D(﹣1,﹣![]() ),直线l的解析式为y=﹣x,
),直线l的解析式为y=﹣x,
∴直线DH的解析式为y=x﹣![]() ,
,
由 ,解得
,解得![]() ,
,
∴H(![]() ,﹣
,﹣![]() ),M(0,
),M(0,![]() ),
),
∴DH=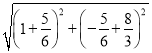 =
=![]() ,
,
∵DG=﹣![]() +
+![]() =
=![]() ,
,
∴![]() 的最小值=
的最小值=![]() =
=![]() .
.
(3)如图2中,连接BM,延长FA交y轴于J.
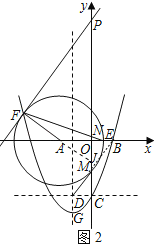
∵A(﹣2,0),M(0,﹣![]() ),
),
∴AM=AF=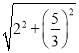 =
=![]() ,
,
∵B(1,0),
∴直线BM的解析式为y=![]() x﹣
x﹣![]() ,
,
∵PF是⊙A的切线,
∴PF⊥AF,
∵PF∥BM,
∴AF⊥BM,
∴直线AF的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
∴J(0,﹣![]() ),
),
∴AJ=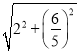 =
=![]() ,
,
∴FJ=AF+AJ=![]() ,
,
∵PF∥BM,
∴∠FPJ=∠OMB,
∴tan∠FPJ=tan∠OMB,
∴![]() =
=![]() ,
,
∴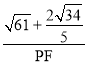 =
=![]() ,
,
∴PF=![]() ,
,
∵AF=AE,
∴∠AFE=∠AEF,
∵∠AFE+∠PFN=90°,∠AEN+∠ONE=90°,∠PNF=∠ENO,
∴∠PFN=∠PNF,
∴PN=PF=![]() .
.

【题目】为提升学生的数学素养,某学校开展了“数学素养”竞赛活动.九年级![]() 名学生参加了竞赛,结果所有学生成绩都不低于
名学生参加了竞赛,结果所有学生成绩都不低于![]() 分(满分
分(满分![]() 分).为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表,根据表中所给信息,解答下列问题:
分).为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表,根据表中所给信息,解答下列问题:
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
![]() 表中
表中![]() ___ _ _ ,
___ _ _ ,![]() _;
_;
![]() 这组数据的中位数落在_____ _范围内;
这组数据的中位数落在_____ _范围内;
![]() 若成绩不小于
若成绩不小于![]() 分为优秀,请估计九年级大约有多少名学生获得优秀成绩?
分为优秀,请估计九年级大约有多少名学生获得优秀成绩?
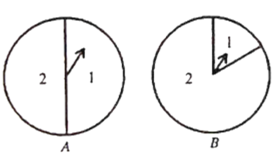
![]() 竞赛中有这样一道题目: 如图,有两个转盘
竞赛中有这样一道题目: 如图,有两个转盘![]() 在每个转盘各自的两个扇形区域中分别标有数字1,2,分别转动转盘
在每个转盘各自的两个扇形区域中分别标有数字1,2,分别转动转盘![]() 当转盘停止转动时,若事件“指针都落在标有数字
当转盘停止转动时,若事件“指针都落在标有数字![]() 的扇形区域内”概率是
的扇形区域内”概率是![]() ,则转盘
,则转盘![]() 中标有数字
中标有数字![]() 的扇形的圆心角的度数是 .
的扇形的圆心角的度数是 .