��Ŀ����
����Ŀ��ÿ���3��15����������������Ȩ������������Ҿ��̳Ƕ�����������������д��۴����.�����ҵ�ij��ɳ��ÿ�׳ɱ�Ϊ5000Ԫ���ڱ��8000Ԫ�Ļ����ϴ�9������.
��1�����ڼ�����������������������������ཱུ�۶���Ԫ������ʹ�����ʲ�����20%��
��2����ý�屬�ϣ���һЩ�����������Ʒ�۸���ٽ��۴�����������թ��Ϊ.������Ҳ������ͬ��ɳ������ɱ�������������һ�£���ǰÿ�ܿ��۳�8�ף����������Ƚ�������![]() ���ٴ������
���ٴ������![]() Ԫ��ʹ�����ɳ����3��15����һ�������������ͱ�ԭ��һ������������������
Ԫ��ʹ�����ɳ����3��15����һ�������������ͱ�ԭ��һ������������������![]() ������һ�������ﵽ��50000Ԫ����
������һ�������ﵽ��50000Ԫ����![]() ��ֵ.
��ֵ.
���𰸡���1��1200����2��50
��������
��1���轵��xԪ������ʹ�����ʲ�����20%�������ۼ�-�ɱ�=�����ɵó�����x��һԪһ�β���ʽ����֮���ɵó�m��ȡֵ��Χ��ȡ�����ֵ���ɵó����ۣ�
��2������������=�����������������������ɵó�����m��һԪ���η��̣���֮ȡ����ֵ���ɵó����ۣ�
�⣺��1���轵��![]() Ԫ������ʹ�����ʲ�����20%��
Ԫ������ʹ�����ʲ�����20%��
��������ã�![]() ��
��
��ã�![]() ��
��
����ཱུ��1200Ԫ������ʹ�����ʲ�����20%��
��2����������ã�![]()
�����ã�![]() ��
��
��ã�![]() ��
��![]() ���������⣬��ȥ����
���������⣬��ȥ����
��![]() ��ֵΪ50��
��ֵΪ50��

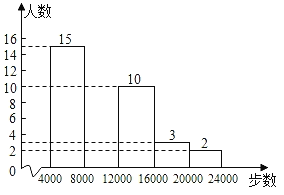
����Ŀ����������˶�����Խ��Խ����˹�ע��ϲ����ij��ѧ��ȤС����������˸�У50����ʦij�ա����˶����е����߲������������ͳ�Ƶ����ݻ��Ƴ�������������������ͳ��ͼ���������������Ϣ������������⣺
��1�����a��b��c��d��ֵ������ȫƵ���ֲ�ֱ��ͼ��
��2������Լ��58000����ʦ���õ�����������ݹ������в�������12000��������12000�����Ľ�ʦ�ж�������
��3�����ڱ������50����ʦ�У�ѡȡ���в�������16000��������16000������������ʦ���ҷ����ĵã���ѡȡ��������ʦ�������߲���ǡ�ö���20000��������20000�������ϵĸ��ʣ�
������x�� | Ƶ�� | Ƶ�� |
0��x��4000 | a | 0.16 |
4000��x��8000 | 15 | 0.3 |
8000��x��12000 | b | 0.24 |
12000��x��16000 | 10 | c |
16000��x��20000 | 3 | 0.06 |
2000��x��24000 | 2 | d |