题目内容
【题目】如图,![]() ,
,![]() ,
,![]() ,
,![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
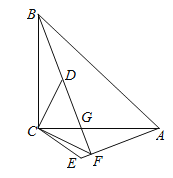
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)请判断![]() 与
与![]() 的大小关系并说明理由.
的大小关系并说明理由.
【答案】(1)见详解;(2)见详解;(3)∠CFE=∠CAB;理由见详解.
【解析】
(1)根据垂直的定义得到∠ACB=∠DCE=90°,由角的和差得到∠BCD=∠ACE,即可得到结论;
(2)根据全等三角形的性质得到∠CBD=∠CAE,根据对顶角的性质得到∠BGC=∠AGF,由三角形的内角和即可得到结论;
(3)过C作CH⊥AE于H,CI⊥BF于I,根据全等三角形的性质得到AE=BD,S△ACE=S△BCD,根据三角形的面积公式得到CH=CI,于是得到CF平分∠BFH,推出△ABC是等腰直角三角形,即可得到结论.
证明:(1)∵BC⊥CA,DC⊥CE,
∴∠ACB=∠DCE=90°,
∵∠ACB-∠ACD=∠DCE-∠ACD,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
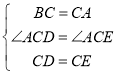 ,
,
∴△ACE≌△BCD;
(2)∵△BCD≌△ACE,
∴∠CBD=∠CAE,
∵∠BGC=∠AGF,
∴∠AFB=∠ACB=90°,
∴BF⊥AE;
(3)∠CFE=∠CAB;
理由如下:过C作CH⊥AE于H,CI⊥BF于I,
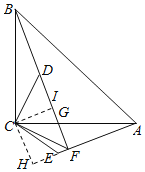
∵△BCD≌△ACE,
∴AE=BD,S△ACE=S△BCD,
即![]() ,
,
∴CH=CI,
∴CF平分∠BFH,
∵BF⊥AE,
∴∠BFH=90°,∠CFE=45°,
∵BC⊥CA,BC=CA,
∴△ABC是等腰直角三角形,
∴∠CAB=45°,
∴∠CFE=∠CAB.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目