题目内容
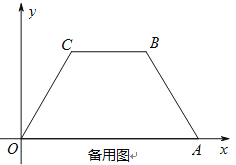
【题目】如图,在平面直角坐标系中,四边形OABC是等腰梯形,BC∥OA,OA=7,AB=4,∠ COA=60°,点P为x轴上的—个动点,点P不与点O、点A重合.连结CP,过点P作PD交AB于点D.
(1)求点B的坐标;
(2)当点P运动什么位置时,△OCP为等腰三角形,求这时点P的坐标;
(3)当点P运动什么位置时,使得∠CPD=∠OAB,且![]() =
=![]() ,求这时点P的坐标。
,求这时点P的坐标。

【答案】(1)B(5, ![]() );(2)P(4,0)或P(-4,0);(3)P(1,0)或P(6,0)
);(2)P(4,0)或P(-4,0);(3)P(1,0)或P(6,0)
【解析】解:(1)过C作CM⊥x轴,垂足M,过B作BN⊥x轴,垂足N
因为四边形OABC是等腰梯形,AB=4, ∠COA=60°
故:OC=AB=4,∠OAB=60°,AN=OM,CM=BN
故:OM=1/2OC=2=AN,CM=2√3=BN
因为BC//OA,OA=7
故:MN=OA-OM-AN=3
故:ON=OM+MN=5
故:B(5,2√3)
(2)如果△OCP为等腰三角形,因为∠COA=60°
则:△OCP为正三角形或P在x轴的负半轴上
①当△OCP为正三角形时
故:OP=OC=4
故:P(4,0)
②P在x轴的负半轴上时
也有OP=OC=4
故:P(-4,0)
(3)∠CPD=∠OAB=∠COA =60°
故:∠OPC+∠DPA=∠DPA+∠ADP=120°
故:∠OPC=∠ADP
故:△OPC∽△ADP
故:OP/AD=OC/PA
因为8*BD=5*AB, AB=4
故:BD=5/2
故:AD=AB-BD=3/2
设OP =x,故:PA=OA-OP=7-x
故:x/(3/2)=4/(7-x)
故:x=1或x=6
故:P(1,0)或P(6,0)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目