题目内容
【题目】（1）阅读理解：
我们知道，只用直尺和圆规不能解决的三个经典的希腊问题之一是三等分任意角，但是这个任务可以借助如图1所示的一边上有刻度的勾尺完成，勾尺的直角顶点为P，
“宽臂”的宽度＝PQ＝QR＝RS，（这个条件很重要哦！）勾尺的一边MN满足M，N，Q三点共线（所以PQ⊥MN）．
下面以三等分∠ABC为例说明利用勾尺三等分锐角的过程：
第一步：画直线DE使DE∥BC，且这两条平行线的距离等于PQ；
第二步：移动勾尺到合适位置，使其顶点P落在DE上，使勾尺的MN边经过点B，同时让点R落在∠ABC的BA边上；
第三步：标记此时点Q和点P所在位置，作射线BQ和射线BP．
请完成第三步操作，图中∠ABC的三等分线是射线 、 ．
（2）在（1）的条件下补全三等分∠ABC的主要证明过程：
∵ ，BQ⊥PR，
∴BP＝BR．（线段垂直平分线上的点与这条线段两个端点的距离相等）
∴∠ ＝∠ ．
∵PQ⊥MN，PT⊥BC，PT＝PQ，
∴∠ ＝∠ ．
（角的内部到角的两边距离相等的点在角的平分线上）
∴∠ ＝∠ ＝∠ ．
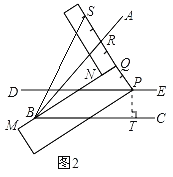
（3）在（1）的条件下探究：
是否成立？如果成立，请说明理由；如果不成立，请在图2中∠ABC的外部画出
（无需写画法，保留画图痕迹即可）．
【答案】（1）作图见解析， BP、BQ；（2）PQ＝QR，ABQ，PBQ，PBQ，PBC，ABQ，PBQ，PBC；（3）不成立，图见解析.
【解析】
（1）根据题意和作法即可补全图形，进而对∠ABC的三等分线进行判断；
（2）根据线段垂直平分线的性质、等腰三角形三线合一的性质、角平分线的判定依次进行判断填写即可；
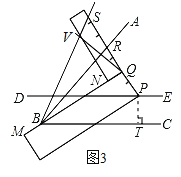
（3）连接BS，如图2，
不成立，如图3，作点Q关于直线AB的对称点V，作射线BV，即为所求.
解：（1）如图1，∠ABC的三等分线是射线BP、射线BQ；故答案为：BP，BQ；
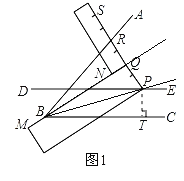
（2）如图1，作PT⊥BC于点T，∵PQ＝QR，BQ⊥PR，
∴BP＝BR．（线段垂直平分线上的点与这条线段两个端点的距离相等）
∴∠ABQ＝∠PBQ．
∵PQ⊥MN，PT⊥BC，PT＝PQ，
∴∠PBQ＝∠PBC．（角的内部到角的两边距离相等的点在角的平分线上）
∴∠ABQ＝∠PBQ＝∠PBC．
故答案为： PQ＝QR，ABQ，PBQ，PBQ，PBC，ABQ，PBQ，PBC；
（3）在（1）的条件下，连接BS，如图2，∠ABS≠∠ABQ，所以∠ABS＝
∠ABC不成立；
如图3，作点Q关于直线AB的对称点V，作射线BV，则∠ABV满足∠ABV＝∠ABQ＝∠ABC，且在∠ABC外部，符合题意．
