题目内容
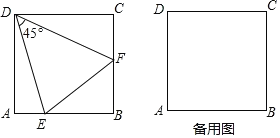
【题目】如图,在正方形ABCD中,E为直线AB上的动点(不与A,B重合),作射线DE并绕点D逆时针旋转45°,交直线BC边于点F,连结EF.
探究:当点E在边AB上,求证:EF=AE+CF.
应用:(1)当点E在边AB上,且AD=2时,则△BEF的周长是______.
(2)当点E不在边AB上时,EF,AE,CF三者的数量关系是______.
【答案】4EF=CF-AE或EF=AE-CF
【解析】
探究:作辅助线,构建全等三角形,证明△DAG≌△DCF(SAS),得∠1=∠3,DG=DF,再证明△GDE≌△FDE(SAS),根据EG的长可得结论;
应用:
(1)利用探究的结论计算三角形周长为4;
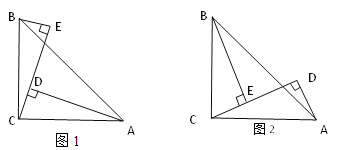
(2)分两种情况:①点E在BA的延长线上时,如图2,EF=CF-AE,②当点E在AB的延长线上时,如图3,
EF=AE-CF,两种情况都是作辅助线,构建全等三角形,证明两三角形全等得线段相等,根据线段的和与差得出结论.
探究:证明:如图,延长BA到G,使AG=CF,连接DG,
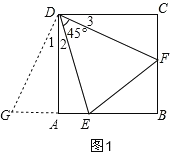
∵四边形ABCD是正方形,
∴DA=DC,∠DAG=∠DCF=90°,
∴△DAG≌△DCF(SAS),
∴∠1=∠3,DG=DF,
∵∠ADC=90°,∠EDF=45°,
∴∠EDG=∠1+∠2=∠3+∠2=45°=∠EDF,
∵DE=DE,
∴△GDE≌△FDE(SAS),
∴EF=EG=AE+AG=AE+CF;
应用:
(1)△BEF的周长=BE+BF+EF ,
由探究得:EF=AE+CF,
∴△BEF的周长=BE+BF+AE+CF=AB+BC=2+2=4,
故答案为:4;
(2)当点E不在边AB上时,分两种情况:
①点E在BA的延长线上时,如图2,
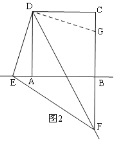
EF=CF-AE,理由是:
在CB上取CG=AE,连接DG,
∵∠DAE=∠DCG=90°,AD=DC,
∴△DAE≌△DCG(SAS)
∴DE=DG,∠EDA=∠GDC
∵∠ADC=90°,
∴∠EDG=90°
∴∠EDF+∠FDG=90°,
∵∠EDF=45°,
∴∠FDG=90°-45°=45°,
∴∠EDF=∠FDG=45°,
在△EDF和△GDF中,
∵DE=DG,∠EDF=∠GDF,DF=DF
∴△EDF≌△GDF(SAS),
∴EF=FG,
∴EF=CF-CG=CF-AE;
②当点E在AB的延长线上时,如图3,
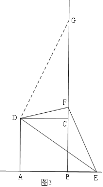
EF=AE-CF,理由是:
延长BC到G,使CG=AE, 连接DG,
∵DA=DC,∠DAE=∠DCG=90°, CG=AE
∴△DAE≌△DCG
∴DE=DG, ∠ADE=∠CDG.
∴∠ADE+∠EDC=∠CDG+∠EDC=90.
即:∠ADC=∠EDG=90,
∵∠EDF=45°,
∴∠GDF=90°-45°=45°,
∴∠EDF=∠GDF,
∵DF=DF,∠EDF=∠GDF,DE=DG
∴△EDF≌△GDF,
∴EF=GF,
∴EF=CG-CF=AE-CF;
综上所述,当点E不在边AB上时,EF,AE,CF三者的数量关系是:EF=CF-AE或EF=AE-CF;

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案