题目内容
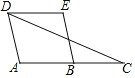
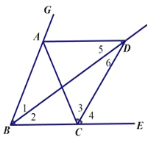
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:AB=AD;
(2)求证:CD平分∠ACE.
(3)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

【答案】(1)证明见解析;(2)证明见解析;(3)∠BDC=![]() ∠BAC,证明见解析
∠BAC,证明见解析
【解析】
(1)根据平行线的性质得到∠ADB=∠DBC,由角平分线的定义得到∠ABD=∠DBC,等量代换得到∠ABD=∠ADB,根据等腰三角形的判定即可得到AB=AD;(2)根据平行线的性质得到∠ADC=∠DCE,由①知AB=AD,等量代换得到AC=AD,根据等腰三角形的性质得到∠ACD=∠ADC,求得∠ACD=∠DCE,即可得到结论;
(3)根据角平分线的定义得到∠DBC=![]() ∠ABC,∠DCE=
∠ABC,∠DCE=![]() ∠ACE,由于∠BDC+∠DBC=∠DCE于是得到∠BDC+
∠ACE,由于∠BDC+∠DBC=∠DCE于是得到∠BDC+![]() ∠ABC=∠ACE,由∠BAC+∠ABC=∠ACE,于是得到∠BDC+
∠ABC=∠ACE,由∠BAC+∠ABC=∠ACE,于是得到∠BDC+![]() ∠ABC=
∠ABC=![]() ∠ABC+
∠ABC+![]() ∠BAC,即可得到结论.
∠BAC,即可得到结论.
证明:
![]() (1) AD∥BE
(1) AD∥BE
![]() ∠2= ∠5
∠2= ∠5
![]() AD平分∠GBE
AD平分∠GBE
![]() ∠2= ∠1
∠2= ∠1
![]() ∠1= ∠5 , AB= AD
∠1= ∠5 , AB= AD
(2) ![]() AB= AD AB= ACAC= AD
AB= AD AB= ACAC= AD
![]() ∠3= ∠ADC
∠3= ∠ADC
![]() 又AD∥BE ∠ADC= ∠4
又AD∥BE ∠ADC= ∠4
![]() ∠3= ∠4
∠3= ∠4
![]() CD平分∠ACE
CD平分∠ACE
(3)∠BDC=![]() ∠BAC
∠BAC
![]()
![]() 证明:BD平分∠ABE
证明:BD平分∠ABE
∴∠2= ∠1 = ![]() ∠ABC
∠ABC
根据三角形外角性质得:
∠1+ ∠2+ ∠BAC=∠4 +∠3①
①式两边除以2得![]() ∠BAC=∠4-∠2
∠BAC=∠4-∠2
而由∠2+ ∠6 =∠4 得出∠6 =∠4 -∠2 即∠BDC=∠4 -∠2
∠BDC=![]() ∠BAC
∠BAC

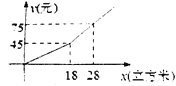
【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x | ··· | 1 | 2 | 3 | 5 | 7 | 9 | ··· |
y | ··· | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ··· |
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为________;
②该函数的一条性质:__________________.