题目内容
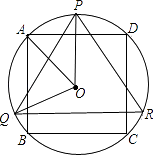
【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.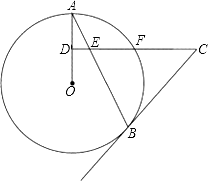
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果BE=10,sinA= ![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】
(1)证明:连接OB 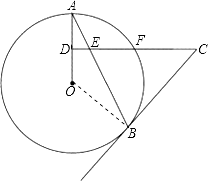
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC
又∵CD⊥OA
∴∠A+∠AED=∠A+∠CEB=90°
∴∠OBA+∠ABC=90°
∴OB⊥BC
∴BC是⊙O的切线
(2)解:连接OF,AF,BF, 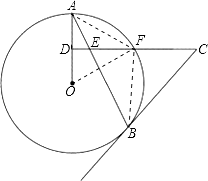
∵DA=DO,CD⊥OA,
∴AF=OF,
∵OA=OF,
∴△OAF是等边三角形,
∴∠AOF=60°
∴∠ABF= ![]() ∠AOF=30°
∠AOF=30°
(3)解:连接OF,AF, 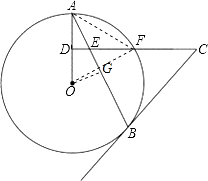
∵DA=DO,CD⊥OA,
∴AF=OF=OA,
过点O作OG⊥AB于点G,得到AG=BG,
在Rt△AOG中,sinA= ![]() =
= ![]() ,
,
设DE=5x,则AE=13x,AD=12x,AO=24x,
∵BE=10,∴AB=10+13x.
则AG= ![]() AB=5+
AB=5+ ![]() x,
x,
又∵直角△AOG中,sin∠BAO= ![]() ,则
,则 ![]() =
= ![]() ,
,
则 ![]() =
= ![]()
解得x= ![]() ,
,
∴AO=24x= ![]() .
.
【解析】(1)根据等边对等角,得到∠A=∠OBA,∠CEB=∠ABC,又CD⊥OA,由角的和差得到OB⊥BC,根据切线的判定方法得出BC是⊙O的切线;(2)根据垂直平分线定理,得到AF=OF,又OA=OF,得到△OAF是等边三角形,∠AOF=60°,所以∠ABF= ![]() ∠AOF=30°;(3)由DA=DO,CD⊥OA,得到AF=OF=OA,过点O作OG⊥AB于点G,得到AG=BG,在Rt△AOG中,sinA=
∠AOF=30°;(3)由DA=DO,CD⊥OA,得到AF=OF=OA,过点O作OG⊥AB于点G,得到AG=BG,在Rt△AOG中,sinA= ![]() ,由BE=10,得到AG=
,由BE=10,得到AG= ![]() AB,又直角△AOG中,sin∠BAO=
AB,又直角△AOG中,sin∠BAO= ![]() ,则
,则 ![]() =
= ![]()
![]() ,求出AO的值.
,求出AO的值.

【题目】近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?