Question

【题目】已知点A，B分别在反比例函数y= （x＞0），y= （x＞0）的图象上且OA⊥OB，则tanB为（ ）

A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：法一：

设点A的坐标为（x1， ），点B的坐标为（x2，﹣ ），

设线段OA所在的直线的解析式为：y=k1x，线段OB所在的直线的解析式为：y=k2x，

则k1= ，k2=﹣ ，

∵OA⊥OB，

∴k1k2= （﹣ ）=﹣1

整理得：（x1x2）2=16，

∴tanB= = = = = = = ．

法二：过点A作AM⊥y轴于点M，过点B作BN⊥y轴于点N，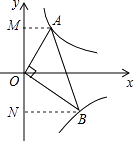

∴∠AMO=∠BNO=90°，

∴∠AOM+∠PAM=90°，

∵OA⊥OB，

∴∠AOM+∠BON=90°，

∴∠AOM=∠BON，

∴△AOM∽△OBN，

∵点A，B分别在反比例函数y= （x＞0），y= （x＞0）的图象上，

∴S△AOM：S△BON=1：4，

∴AO：BO=1：2，

∴tanB= ．

所以答案是：B．

【考点精析】关于本题考查的相似三角形的判定与性质和特殊角的三角函数值，需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方；分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”才能得出正确答案．