题目内容
【题目】如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=( )
A.60°
B.65°
C.72°
D.75°
【答案】D
【解析】解:连接OD,AR,
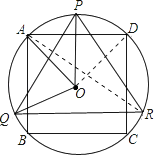
∵△PQR是⊙O的内接正三角形,
∴∠PRQ=60°,
∴∠POQ=2×∠PRQ=120°,
∵四边形ABCD是⊙O的内接正方形,
∴△AOD为等腰直角三角形,
∴∠AOD=90°,
∵BC∥RQ,AD∥BC,
∴AD∥QR,
∴∠ARQ=∠DAR,
∴弧AQ=弧DR,
∵△PQR是等边三角形,
∴PQ=PR,
∴弧PQ=弧PR,
∴弧AP=弧PD,
∴∠AOP= ![]() ∠AOD=45°,
∠AOD=45°,
所以∠AOQ=∠POQ﹣∠AOP=120°﹣45°=75°.
所以答案是:D.
【考点精析】解答此题的关键在于理解正多边形和圆的相关知识,掌握圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等.

练习册系列答案
相关题目