题目内容
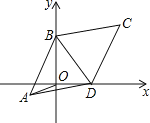
【题目】如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是 .
【答案】![]() .
.
【解析】
试题分析:此题主要考查了菱形的性质以及等边三角形的判定与性质,得出当点A,O,E在一条直线上,此时AO最短是解题关键.利用菱形的性质以及等边三角形的性质得出A点位置,进而求出AO的长.
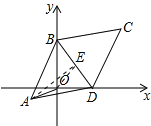
试题解析:如图所示:过点A作AE⊥BD于点E, 当点A,O,E在一条直线上,此时AO最短,
∵菱形ABCD中,BC=10,∠BCD=60°,
∴AB=AD=CD=BC=10,∠BAD=∠BCD=60°,
∴△ABD是等边三角形,
∴AE过点O,E为BD中点,则此时EO=5,
故AO的最小值为:AO=AE-EO=ABsin60°-![]() ×BD=5
×BD=5![]() -5.
-5.
故答案为5![]() -5
-5

练习册系列答案
相关题目