题目内容
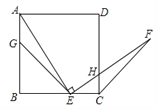
【题目】如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=![]() GE;②△AGE≌△ECF;③∠FCD=45°;④BE=
GE;②△AGE≌△ECF;③∠FCD=45°;④BE=![]() GE.其中,正确的结论有( )
GE.其中,正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】∵四边形ABCD是正方形,
∴∠B=∠DCB=90°,AB=BC,
∵AG=CE,
∴BG=BE,
由勾股定理得:BE=![]() GE,∴①错误,④正确;
GE,∴①错误,④正确;
∵BG=BE,∠B=90°,
∴∠BGE=∠BEG=45°,
∴∠AGE=135°,
∴∠GAE+∠AEG=45°,
∵AE⊥EF,
∴∠AEF=90°,
∵∠BEG=45°,
∴∠AEG+∠FEC=45°,
∴∠GAE=∠FEC,
在△GAE和△CEF中

∴△GAE≌△CEF,∴②正确;
∴∠AGE=∠ECF=135°,
∴∠FCD=135°90°=45°,∴③正确;
即正确的有3个.
故选C.
点睛:本题考查了正方形的性质,等腰三角形的性质,全等三角形的性质,相似三角形的判定,勾股定理等知识点的综合运用,综合比较强,难度较大.

练习册系列答案
相关题目
【题目】小明靠勤工俭学的收入维持上大学的费用,下面是小明一周的收支情况表(收入为正,单位:元)
周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
+15 | +10 | 0 | +20 | +15 | +10 | +14 |
-8 | -12 | -19 | -10 | -9 | -11 | -8 |
(1)在一周内小明有多少节余;
(2)照这样一个月(按30天计算)小明能有多少节余;
(3)按以上支出,小明一个月(按30天计算)至少要赚多少钱,才以维持正常开支.