题目内容
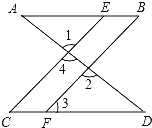
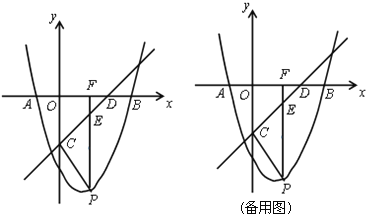
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A(-1,0)、B(3,0)两点,直线y=x-2与x轴交于点D,与y轴交于点C.点P是x轴下方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
与x轴交于点A(-1,0)、B(3,0)两点,直线y=x-2与x轴交于点D,与y轴交于点C.点P是x轴下方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式:
(2)若PE=3EF,求m的值;
(3)连接PC,是否存在点P,使△PCE为等腰直角三角形?若存在,请直接写出相应的点P的横坐标m的值;若不存在,请说明理由.
【答案】(1)y=x2-2x-3;(2)m=1或m=![]() ;(3)m=1±
;(3)m=1±![]() ,或
,或![]() 或
或![]() .
.
【解析】
试题分析:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,二次函数图象上点的坐标特征,等腰直角三角形的性质,难点在于(3)判断出直线CD与y轴的夹角为45°并分情况讨论.
(1)将点A、B的坐标代入抛物线求出a、b,即可得解;
(2)根据抛物线解析式与直线解析式表示出点P、E的坐标,然后表示出PE、EF,再列出绝对值方程,然后求解即可;
(3)根据直线解析式求出直线CD与y轴的夹角为45°,然后分①∠PCE=90°时表示出PC的解析式,再与抛物线解析式联立求解即可;②∠CPE=90°时,PC∥x轴,点P与点C的纵坐标相等,然后根据抛物线解析式求解即可.
试题解析:(1)把A(-1,0)、B(3,0),两点的坐标代入y=ax2+bx-3得:![]() ,
,
解得:![]() ,
,
所以,这条抛物线的解析这式为:y=x2-2x-3;
(2)设点P的横坐标是m,则P(m,m2-2m-3),E(m,m-2),F(m,0),
PE=|yE-yP|=|(m-2)-(m2-2m-3)|=|-m2+3m+1|,
EF=|-m+2|,
由题意PE=3EF,即:|-m2+3m+1|=3|-m+2|,
①若-m2+3m+1=3(-m+2),整理得:m
②若-m2+3m+1=-3(-m+2),整理得:m2-7=0,
解得:m=7或m=-7,
∵P在x轴下方,
∴-1<m<3,m=-7不合题意应舍去,
∴m=7,
综上所述,m=1或m=7;
(3)存在点P的横坐标为:m=1-![]() 或
或![]() 或
或![]() .
.
理由如下:直线y=x-2与y轴的夹角为45°,
①PCE=90°时,直线PC的解析式为y=-x-2,
联立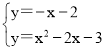 ,
,
消掉y得,x2-x-1=0,
解得x=![]() 或
或![]() ,
,
所以,点P的横坐标m=![]() 或
或![]() ;
;
②∠CPE=90°时,PC∥x轴,
∵点C(0,-2),
∴点P与点C的纵坐标相等,为-2,
∴x2-2x-3=-2,
解得x=1±![]() ,
,
∵点P是x轴下方的抛物线上一动点,
∴-1<x<3,
∴点P的横坐标m=1±![]() ,
,
综上所述,点P的横坐标m=1±![]() 或
或![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案