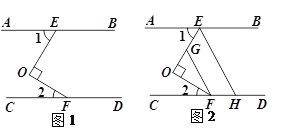题目内容
【题目】完成以下证明,并在括号内填写理由.
已知:如图所示,∠1=∠2,∠A=∠3.
求证:∠ABC+∠4+∠D=180°.
证明:∵∠1=∠2
∴ ∥ ( )
∴∠A=∠4( )
∠ABC+∠BCE=180°( )
即∠ABC+∠ACB+∠4=180°
∵∠A=∠3
∴∠3=
∴ ∥
∴∠ACB=∠D( )
∴∠ABC+∠4+∠D=180°
【答案】答案见解析
【解析】试题分析:根据题意,结合图形,由平行线的判定与性质可填空.
试题解析:证明:∵∠1=∠2
∴ AB ∥ CE ( 内错角相等,两直线平行)
∴∠A=∠4( 两直线平行,内错角相等 )
∠ABC+∠BCE=180°( 两直线平行,同旁内角互补 )
即∠ABC+∠ACB+∠4=180°
∵∠A=∠3
∴∠3= ∠4
∴AC∥ DE
∴∠ACB=∠D( 两直线平行,同位角相等 )
∴∠ABC+∠4+∠D=180°

练习册系列答案
相关题目