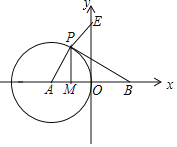题目内容
【题目】如图,平行四边形![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,现将
,现将![]() 沿直线
沿直线![]() 翻折至
翻折至![]() 的位置,
的位置,![]() 与
与![]() 交于点
交于点![]() .
.
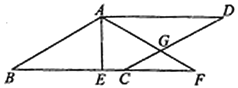
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据平行四边形的性质得AB∥CD,AB=CD,通过两角对应相等证明△FCG∽△FBA,利用对应边成比例列比例式,进行等量代换后化等积式即可;
(2)根据直角三角形30°角所对的直角边等于斜边的一半及勾股定理,求出BE的长,再由折叠性质求出BF长,结合(1)的结论代入数据求解.
解(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,AD=BC
∴∠GCF=∠B, ∠CGF=∠BAF,
∴△FCG∽△FBA,
∴![]() ,
,
∴![]()
∴![]() .
.
(2)∵![]() ,
,
∴∠AEB=90°,
∵∠B=30°, ![]() ,
,
∴AE=![]() ,
,
由勾股定理得,BE=6,
由折叠可得,BF=2BE=12,
∵AD=BC=8,
∴CF=4
∵![]() ,
,
∴![]() ,
,
∴CG=![]() ,
,
∴DG=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
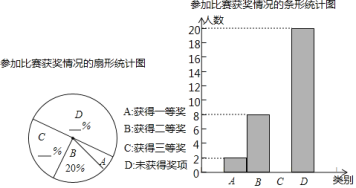
【题目】为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下(成绩得分均为整数):
组别 | 成绩分组 | 频数频率 | 频数 |
1 |
| 2 | 0.05 |
2 |
| 4 | 0.10 |
3 |
|
| 0.2 |
4 |
| 10 | 0.25 |
5 |
|
|
|
6 |
| 6 | 0.15 |
合计 | 40 | 1.00 |
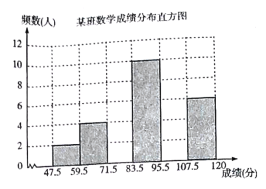
根据表中提供的信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ,
,![]() ;
;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 ,72分及以上为及格,预计及格的人数约为 ,及格的百分比约为 ;
(3)补充完整频数分布直方图.