题目内容
【题目】数学活动﹣旋转变换
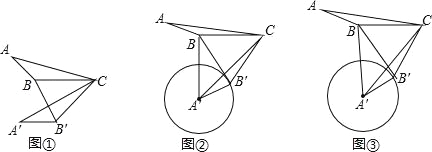
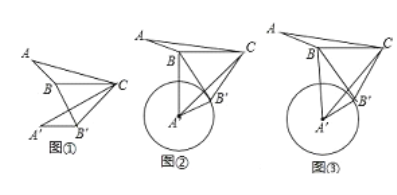
（1）如图①，在△ABC中，∠ABC=130°，将△ABC绕点C逆时针旋转50°得到△A′B′C，连接BB′，求∠A′B′B的大小；
（2）如图②，在△ABC中，∠ABC=150°，AB=3，BC=5，将△ABC绕点C逆时针旋转60°得到△A′B′C，连接BB′，以A′为圆心，A′B′长为半径作圆．
（Ⅰ）猜想：直线BB′与⊙A′的位置关系，并证明你的结论；
（Ⅱ）连接A′B，求线段A′B的长度；
（3）如图③，在△ABC中，∠ABC=α（90°＜α＜180°），AB=m，BC=n，将△ABC绕点C逆时针旋转2β角度（0°＜2β＜180°）得到△A′B′C，连接A′B和BB′，以A′为圆心，A′B′长为半径作圆，问：角α与角β满足什么条件时，直线BB′与⊙A′相切，请说明理由，并求此条件下线段A′B的长度（结果用角α或角β的三角函数及字母m、n所组成的式子表示）
【答案】(1)65°；（2）（Ⅰ）结论：直线BB′、是⊙A′的切线，理由详见解析；（Ⅱ）
；（3）
.
【解析】
试题分析：（1）由旋转的性质可得∠A′B′C=∠ABC=130°，CB=CB′，根据等腰三角形的性质和三角形的内角和定理即可求得∠A′B′B得度数；（2）（Ⅰ）结论：直线BB′是⊙A′的切线．根据已知条件证明∠A′B′B=90°，即可判定直线BB′是⊙A′的切线；（Ⅱ）在RT△ABB′中，根据勾股定理即可计算出线段A′B的长度；（3）如图③中，当α+β=180°时，直线BB′、是⊙A′的切线．只要证明∠A′B′B=90°即可解决问题．在△CBB′中求出BB′，再在RT△A′B′B中利用勾股定理即可．
试题解析：（1）如图①中，∵△A′B′C是由△ABC旋转得到，
∴∠A′B′C=∠ABC=130°，CB=CB′，
∴∠CBB′=∠CB′B，∵∠BCB′=50°，
∴∠CBB′=∠CB′B=65°，
∴∠A′B′B=∠A′B′C﹣∠BB′C=65°．
（2）（Ⅰ）结论：直线BB′、是⊙A′的切线．
理由：如图②中，∵∠A′B′C=∠ABC=150°，CB=CB′，
∴∠CBB′=∠CB′B，∵∠BCB′=60°，
∴∠CBB′=∠CB′B=60°，
∴∠A′B′B=∠A′B′C﹣∠BB′C=90°．
∴AB′⊥BB′，
∴直线BB′是⊙A′的切线．
（Ⅱ）∵在RT△ABB′中，∵∠AB′B=90°，BB′=BC=5，AB′=AB=3，
∴A′B=
=．
（3）如图③中，当α+β=180°时，直线BB′、是⊙A′的切线．
理由：∵∠A′B′C=∠ABC=α，CB=CB′，
∴∠CBB′=∠CB′B，∵∠BCB′=2β，
∴∠CBB′=∠CB′B=
，
∴∠A′B′B=∠A′B′C﹣∠BB′C=α﹣90°+β=180°﹣90°=90°．
∴AB′⊥BB′，
∴直线BB′、是⊙A′的切线．
在△CBB′中∵CB=CB′=n，∠BCB′=2β，
∴BB′=2nsinβ，
在RT△A′BB′中，A′B=
=．
