Question

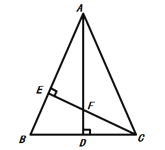
【题目】如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE，求证：

（1）△AEF≌△CEB；

（2）AF=2CD。

Answer 1

【答案】证明见解析.

【解析】试题分析：（1）由AD⊥BC，CE⊥AB，易得∠AFE=∠B，利用全等三角形的判定得△AEF≌△CEB；（2）由全等三角形的性质得AF=BC，由等腰三角形的性质“三线合一”得BC=2CD，等量代换得出结论．

试题解析：（1）证明：由于AB=AC，故△ABC为等腰三角形，∠ABC=∠ACB；

∵AD⊥BC，CE⊥AB，

∴∠AEC=∠BEC=90°，∠ADB=90°；

∴∠BAD+∠ABC=90°，∠ECB+∠ABC=90°，

∴∠BAD=∠ECB，

在Rt△AEF和Rt△CEB中

∠AEF=∠CEB，AE=CE，∠EAF=∠ECB，

所以△AEF≌△CEB（ASA）

（2）∵△ABC为等腰三角形，AD⊥BC，

故BD=CD，

即CB=2CD，

又∵△AEF≌△CEB，

∴AF=CB=2CD。