题目内容
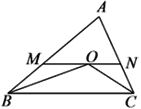
【题目】如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2+∠3＝180°，试说明：∠GDC＝∠B．请补充说明过程，并在括号内填上相应的理由．
解：∵AD⊥BC，EF⊥BC（已知）
∴∠ADB＝∠EFB＝90° ，
∴EF∥AD（ ），
∴ +∠2＝180°（ ）．
又∵∠2+∠3＝180°（已知），
∴∠1＝∠3（ ），
∴AB∥ （ ），
∴∠GDC＝∠B（ ）．
【答案】见解析
【解析】
求出AD∥EF，根据平行线的性质得出∠2+∠1=180°，求出∠1=∠3，根据平行线的判定得出DG∥AB，根据平行线的性质得出∠GDC=∠B即可．
解：∵AD⊥BC，EF⊥BC（已知）
∴∠ADB=∠EFB =90°（ 垂直的定义 ），
∴EF∥AD （同位角相等，两直线平行），
∴ ∠1 +∠2=180°（两直线平行，同旁内角互补）.
又∵∠2+∠3=180°（已知），
∴∠1=∠3 （同角的补角相等），
∴AB∥ DG （内错角相等，两直线平行），
∴∠GDC=∠B （ 两直线平行，同位角相等 ）.
练习册系列答案
相关题目
【题目】某公司有
、
两种型号的客车共20辆，它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下，共载客720人.
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
(1)求、两种型号的客车各有多少辆?
(2)某中学计划租用、两种型号的客车共8辆，同时送七年级师生到沙家浜参加社会实践活动，已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车？
