题目内容
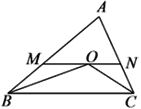
【题目】如图,△ABC中,∠ABC、∠ACB的平分线相交于O,MN过点O且与BC平行.△ABC的周长为20,△AMN的周长为12,则BC的长为( )
A. 10 B. 16 C. 8 D. 4
【答案】C
【解析】
由BO为角平分线,得到一对角相等,再由MN平行于BC,利用两直线平行内错角相等,得到一对角相等,等量代换可得出∠MBO=∠MOB,利用等角对等边得到MO=MB,同理得到NO=NC,而三角形ABC的周长等于三边相加,即AB+BC+AC,其中AB=AM+MB,AC=AN+NC,等量代换后可得出三角形ABC的周长等于三角形AMN的周长与BC的和,即BC等于两三角形的周长之差,将两三角形的周长代入,即可求出BC的长.
解:∵OB平分∠MBC,
∴∠MBO=∠OBC,
又MN∥BC,
∴∠MOB=∠OBC,
∴∠MOB=∠MBO,
∴MB=MO,同理可得∠NOC=∠NCO,
∴NO=NC,
∴(AB+AC+BC)-(AM+AN+MN)
=(AM+MB+AN+NC+BC)-(AM+AN+MN)
=(AM+MO+AN+NO+BC)-(AM+AN+MN)
=(AM+AN+MN+BC)-(AM+AN+MN)
=BC,
又∵△ABC的周长为20,△AMN的周长为12,即AB+AC+BC=20,AM+AN+MN=12,
则BC=20-12=8.
故选:C.

 名校课堂系列答案
名校课堂系列答案【题目】某手机专营店代理销售A、B两种型号手机.手机的进价、售价如下表:
型号 | A | B |
进价 | 1800元/部 | 1500元/部 |
售价 | 2070元/部 | 1800元/部 |
(1)第一个月:用54000元购进A、B两种型号的手机,全部售完后获利9450元,求第一个月购进A、B两种型号手机的数量;
(2)第二个月:计划购进A、B两种型号手机共34部,且不超出第一个月购进A、B两种型号的手机总费用,则A型号手机最多能购多少部?