题目内容
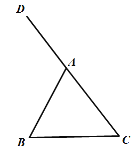
【题目】如图,AB是⊙O的直径,C,D为⊙O上两点,CF⊥AB于点F,CE⊥AD交AD的延长线于点E,且CE=CF. 
(1)求证:CE是⊙O的切线;
(2)连接CD,CB.若AD=CD=a,写出求四边形ABCD面积的思路. 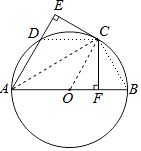
【答案】
(1)解:证明:连接OC,AC.
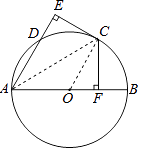
∵CF⊥AB,CE⊥AD,且CE=CF.
∴∠CAE=∠CAB.
∵OC=OA,
∴∠CAB=∠OCA.
∴∠CAE=∠OCA.
∴OC∥AE.
∴∠OCE+∠AEC=180°,
∵∠AEC=90°,
∴∠OCE=90°即OC⊥CE,
∵OC是⊙O的半径,点C为半径外端,
∴CE是⊙O的切线
(2)解:求解思路如下:
①由AD=CD=a,得到∠DAC=∠DCA,于是∠DCA=∠CAB,可知DC∥AB;
![]() =
= ![]() ,
,
②由OC∥AE,OC=OA,可知四边形AOCD是菱形;
③由∠CAE=∠CAB,得到CD=CB,DC=BC=a,可知△OBC为等边三角形;
④由等边△OBC可求高CF的长,进而可求四边形ABCD面积.
解:∵AD=CD,
∴∠DAC=∠DCA=∠CAB,
∴DC∥AB,
∵∠CAE=∠OCA,
∴OC∥AD,
∴四边形AOCD是平行四边形,
∴OC=AD=a,AB=2a,
∵∠CAE=∠CAB,
∴CD=CB=a,
∴CB=OC=OB,
∴△OCB是等边三角形,
在Rt△CFB中,CF= ![]() =
= ![]() ,
,
∴S四边形ABCD= ![]() (DC+AB)CF=
(DC+AB)CF= ![]() a2.
a2.
【解析】(1)连接OC,AC,可先证明AC平分∠BAE,结合圆的性质可证明OC∥AE,可得∠OCB=90°,可证得结论;(2)可先证得四边形AOCD为平行四边形,再证明△OCB为等边三角形,可求得CF、AB,利用梯形的面积公式可求得答案.
【考点精析】本题主要考查了角平分线的性质定理和垂径定理的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.

 中考解读考点精练系列答案
中考解读考点精练系列答案