题目内容
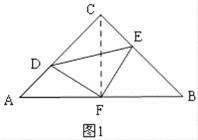
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC、BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动过程中,下列结论:(1)△DFE是等腰直角三角形;(2)DE长度的最小值为4;(3)四边形CDFE的面积保持不变;(4)△CDE面积的最大值是4.正确的结论是( )

A. (1)(2)(3) B. (1)(3)(4) C. (1)(2)(4) D. (2)(3)(4)
【答案】A
【解析】
①连接![]() ,根据已知条件由
,根据已知条件由![]() 可得
可得![]() ,从而可知
,从而可知![]() ,即可对结论(1)(3)作出判断.②当
,即可对结论(1)(3)作出判断.②当![]() 时,
时,![]() 的值最小,此时
的值最小,此时![]() 的值最小,
的值最小,![]() 的最小值为4,故结论(2)正确.③当
的最小值为4,故结论(2)正确.③当![]() 面积最大时,此时
面积最大时,此时![]() 的面积最小,此时S△CDE=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=8,可判断结论(4).
的面积最小,此时S△CDE=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=8,可判断结论(4).
解:(1)连接![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 边上的中点,
边上的中点,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵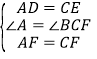 ,
,
∴![]() ),
),
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() 是等腰直角三角形;
是等腰直角三角形;
故(1)正确;
(2)∵![]() ,
,
∴当![]() 时,
时,![]() 的值最小,此时
的值最小,此时![]() 的值最小,
的值最小,![]() 的最小值为4,故(2)正确;
的最小值为4,故(2)正确;
(3)∵![]() ,
,
∴![]() ,
,
∴![]()
∴四边形![]() 的面积保持不变;
的面积保持不变;
故(3)正确;
(4)当![]() 面积最大时,此时
面积最大时,此时![]() 的面积最小,
的面积最小,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
此时S△CDE=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=![]() ,
,
故(4)错误,
故答案为:A.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案【题目】在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体.下面是他测得的弹簧的长度y与所挂物体的质量石的一组对应值:
所挂物体的质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度y/cm | 20 | 22 | 24 | 26 | 25 | 30 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)填空:
①当所挂的物体为3kg时,弹簧长是____.不挂重物时,弹簧长是____.
②当所挂物体的质量为8kg(在弹簧的弹性限度范围内)时,弹簧长度是___.