题目内容
【题目】如图,在平面直角坐标系中,每个小正方形的边长为一个单位长度.已知△ABC的顶点A(-2,5)、B(-4,1)、C(2,3),将△ABC平移得到△A′B′C′,点A(a,b)对应点A′(a+3,b-4)
(1) 画出△A′B′C′并写出点B′、C′的坐标
(2) 试求线段AB在整个平移的过程中在坐标平面上扫过的面积
(3) 在x轴上存在一点P,使得S△ABP=6,则点P的坐标是_____________.

【答案】(1)B'(-1,-3),C'(5,-1);(2)20;(3)(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)根据横坐标+3是向右平移3个单位长度,纵坐标-4是向下平移4个单位长度,画出图形即可;(2)如图:图中阴影面积即线段AB扫过的面积,根据平行四边形面积公式计算即可;(3)过点B作BD⊥x轴于D,过点A作AE⊥x轴于E,可求出梯形AEDB的面积为6,可知P点在D点左侧或在E点右侧,分情况通过梯形和三角形的面积的和与差列方程求出x值即可;
(1)如图:三角形A′B′C′即为所求; B′(-1,-3)、C′(5,-1),设P点坐标为(x,0),
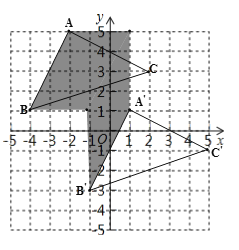
(2) S=3×4+4×2=20;
(3) 过点B作BD⊥x轴于D,过点A作AE⊥x轴于E,设P点坐标为(x,0),
∴S梯形AEDB=![]()
∴P点在D点左侧或E点右侧,
① 当P在E点右侧时,S△ABP=6+![]() ·(x+2)·5-
·(x+2)·5-![]() ·(x+4)·1=6,解得
·(x+4)·1=6,解得![]()
② 当P在D点左侧时,S△ABP=![]() ·(-x-2)·5-6-
·(-x-2)·5-6-![]() ·(-x-4)·1=6,解得
·(-x-4)·1=6,解得![]()
∴P(![]() ,0)或(
,0)或(![]() ,0),
,0),

 导学全程练创优训练系列答案
导学全程练创优训练系列答案【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分2 , 则成绩较为整齐的是队.