题目内容
【题目】如图，在平行四边形ABCD中，∠B＝60°，将△ABC沿对角线AC折叠，点B的对应点落在点E处，且点B，A，E在一条直线上，CE交AD于点F，则图中等边三角形共有( )
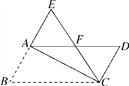
A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】分析：根据折叠的性质可得∠E=∠B=60°，进而可证明△BEC是等边三角形，再根据平行四边形的性质可得：AD∥BC，所以可得∠EAF=60°，进而可证明△EFA是等边三角形，由等边三角形的性质可得∠EFA=∠DFC=60°，又因为∠D=∠B=60°，进而可证明△DFC是等边三角形，问题得解．
详解：∵将△ABC沿对角线AC折叠，点B的对应点落在点E处，
∴∠E=∠B=60°，
∴△BEC是等边三角形，
∵四边形ABCD是平行四边形，
∴AD∥BC，∠D=∠B=60°，
∴∠B=∠EAF=60°，
∴△EFA是等边三角形，
∵∠EFA=∠DFC=60°，∠D=∠B=60°，
∴△DFC是等边三角形，
∴图中等边三角形共有3个，
故选B．
练习册系列答案
相关题目
【题目】某校组织学生到距离学校6千米的科技馆去参观，小华因事没能乘上学校的包车，于是准备在学校门口改乘出租车去科技馆，出租车收费标准有两种类型，如下表：
里程 | 甲类收费（元） | 乙类收费（元） |
3千米以下（包含3千米） | 7.00 | 6.00 |
3千米以上，每增加1千米 | 1.60 | 1.40 |
（1）设出租车行驶的里程为x千米（
且x取正整数），分别写出两种类型的总收费（用含x的代数式表示）；
（2）小华身上仅有11元，他乘出租车到科技馆车费够不够请说明理由．
