题目内容
如图,在等腰梯形ABCD中,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积为______cm2.


方法一:
过点B作BE∥AC,交DC的延长线于点E,又AB∥CE,
∴四边形ACEB是平行四边形,又等腰梯形ABCD
∴BE=AC=DB=6cm,AB=CE,
∵AC⊥BD,
∴BE⊥BD,
∴△DBE是等腰直角三角形,
∴S等腰梯形ABCD=
=
=
=S△DBE=
=6×6÷2
=18(cm2).
方法二:
∵BD是△ADB和△CDB的公共底边,又AC⊥BD,
∴AC=△ADB的高﹢△CDB的高,
∴梯形ABCD的面积=△ADB面积+△CDB面积=
BD×AC=6×
=18(cm2).
故答案为:18.
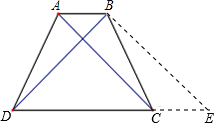
过点B作BE∥AC,交DC的延长线于点E,又AB∥CE,
∴四边形ACEB是平行四边形,又等腰梯形ABCD
∴BE=AC=DB=6cm,AB=CE,
∵AC⊥BD,
∴BE⊥BD,
∴△DBE是等腰直角三角形,
∴S等腰梯形ABCD=
| (AB+DC)h |
| 2 |
=
| (CE+DC)h |
| 2 |
| DE•h |
| 2 |
=S△DBE=
| DB•BE |
| 2 |
=6×6÷2
=18(cm2).
方法二:
∵BD是△ADB和△CDB的公共底边,又AC⊥BD,
∴AC=△ADB的高﹢△CDB的高,
∴梯形ABCD的面积=△ADB面积+△CDB面积=
| 1 |
| 2 |
| 6 |
| 2 |
故答案为:18.


练习册系列答案
相关题目
 D上,将△AEF沿EF翻折,点A的落点记为P.
D上,将△AEF沿EF翻折,点A的落点记为P.





