题目内容
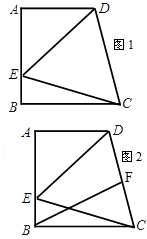
如图，直角梯形纸片ABCD，AD⊥AB，AB=8，AD=CD=4，点E、F分别在线段AB、A
D上，将△AEF沿EF翻折，点A的落点记为P．
（1）当AE=5，P落在线段CD上时，PD=______；
（2）当P落在直角梯形ABCD内部时，PD的最小值等于______．
D上，将△AEF沿EF翻折，点A的落点记为P．（1）当AE=5，P落在线段CD上时，PD=______；
（2）当P落在直角梯形ABCD内部时，PD的最小值等于______．
（1）过P作PG⊥AB于G，则四边形DAGP是矩形，PG=DA=4，
∵PE=AE=5，
∴GE=
=
=3，
∴PD=AG=AE-GE=5-3=2；
（2）连接ED，作P1P⊥ED于P，
那么在Rt△P1PD中，P1D＞PD，
故当点A的对称点P落在线段ED上时，PD有最小值，（左图）
而E在线段AB上，
故当E与B重合时，即EP=BP，此时PD取最小值．（右图）
此时，AB=BP=8，又BD=
=4
，
∴PD=BD-BP=4
-8．
∵PE=AE=5，
∴GE=
| PE2-PG2 |
| 52-42 |
∴PD=AG=AE-GE=5-3=2；
（2）连接ED，作P1P⊥ED于P，
那么在Rt△P1PD中，P1D＞PD，
故当点A的对称点P落在线段ED上时，PD有最小值，（左图）
而E在线段AB上，
故当E与B重合时，即EP=BP，此时PD取最小值．（右图）
此时，AB=BP=8，又BD=
| AB2+AD2 |
| 5 |
∴PD=BD-BP=4
| 5 |
练习册系列答案
阅读快车系列答案
相关题目
