Question

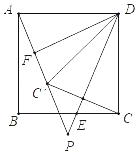
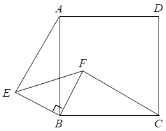
【题目】如图，△EBF为等腰直角三角形，点B为直角顶点， 四边形ABCD是正方形．

⑴ 求证：△ABE≌△CBF；

⑵ CF与AE有什么特殊的位置关系？请证明你的结论．

Answer 1

【答案】（1）见解析；（2）CF⊥AE，理由见解析

【解析】

（1）根据等腰直角三角形的性质得出BE=BF，∠EBF=90°，再根据正方形的性质得出AB=BC，∠ABC=90°，根据余角的性质得到∠EBA=∠CBF，最后根据SAS证明结果；

（2）延长CF，交AE于点G，根据补角的性质得出∠AEB+∠BFG=180°，再根据四边形内角和得出∠EGF+∠EBF=180°，从而可得∠EGF=90°，即可得到结果.

解：（1）∵△EBF为等腰直角三角形，

∴BE=BF，∠EBF=90°，

则∠EBA+∠FBA=90°，

∵四边形ABCD为正方形，

∴AB=BC，∠ABC=90°，则∠ABF+∠CBF=90°，

∴∠EBA=∠CBF，

又∵BE=BF，AB=BC，

∴△ABE≌△CBF（SAS）；

（2）延长CF，交AE于点G，

由（1）得：∠CFB=∠AEB，

∵∠CFB+∠BFG=180°，

∴∠AEB+∠BFG=180°，

∴∠EGF+∠EBF=180°，

∵∠EBF=90°，

∴∠EGF=90°，

∴CF⊥AE.