题目内容
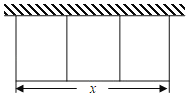
【题目】某农场拟用总长为60m的建筑材料建三间矩形牛饲养室,饲养室的一面靠现有墙(墙长为40m),其中间用建筑材料做的墙隔开(如图).设三间饲养室平行于墙的一边合计用建筑材料xm,总占地面积为ym2.
(1)求y关于x的函数解析式和自变量的取值范围;
(2)当x为何值时,三间饲养室占地总面积最大?最大面积为多少?
【答案】(1)y=﹣![]() x2+15x;0<x≤40;(2)当x=30时,三间饲养室占地总面积最大,最大为225(m2).
x2+15x;0<x≤40;(2)当x=30时,三间饲养室占地总面积最大,最大为225(m2).
【解析】
(1)设饲养室长为x(m),则宽为![]() (60﹣x)m,根据长方形面积公式即可得y关于x的函数解析式,由墙可用长≤40m,可得x的范围;
(60﹣x)m,根据长方形面积公式即可得y关于x的函数解析式,由墙可用长≤40m,可得x的范围;
(2)把函数关系式化成顶点式,然后根据二次函数的性质即可得到结论.
(1)根据题意得,y=x![]() (60﹣x)=﹣
(60﹣x)=﹣![]() x2+15x,
x2+15x,
自变量的取值范围为:0<x≤40;
(2)∵y=﹣![]() x2+15x=﹣
x2+15x=﹣![]() (x﹣30)2+225,
(x﹣30)2+225,
∴当x=30时,三间饲养室占地总面积最大,最大为225(m2).

练习册系列答案
相关题目