题目内容
【题目】如图,将矩形ABCD折叠,使点C与A点重合,折痕为EF.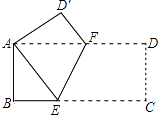
(1)判断四边形AFCE的形状,并说明理由.
(2)若AB=4,BC=8,求折痕EF的长.
【答案】
(1)解:四边形AFCE是菱形,
理由:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
由折叠的性质可得:OA=OC,AE=CE,AF=CF,
在△OAE和△OCF中,
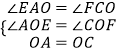 ,
,
∴△AEO≌△CFO(AAS),
∴AE=CF,
∴AE=CE=CF=AF,
∴四边形AFCE是菱形
(2)解:连接AC交EF于点O,
由勾股定理知AC=4 ![]() ,
,
又∵折叠矩形使C与A重合时有EF⊥AC,
则Rt△EOC∽Rt△ABC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴OE= ![]() OC=
OC= ![]() ×2
×2 ![]() ,
,
故EF=2OE=2 ![]() .
.
【解析】(1)抓住已知条件,将矩形ABCD折叠,使点C与A点重合,根据矩形的性质和折叠的性质得出OA=OC,AE=CE,AF=CF,∠EAO=∠FCO,,再证明△AEO≌△CFO,从而得出AE=CF,即可证明四边形AFCE的四边相等,即可得出结论。
(2)根据勾股定理求出AC的长,再证明Rt△EOC∽Rt△ABC,根据相似三角形的对应边成比例,建立方程,求出OE的长,即可得到EF的长。
【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目