题目内容
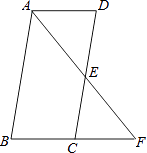
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
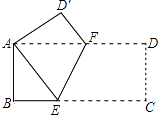
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,求∠HPQ的度数.

【答案】(1)AB∥CD,理由见解析;(2)证明见解析;(3)45°.
【解析】
(1)利用对顶角相等、等量代换可以推知同旁内角∠AEF、∠CFE互补,所以易证AB∥CD;
(2)利用(1)中平行线的性质推知∠BEF+∠EFD=180°;然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG⊥PF,故结合已知条件GH⊥EG,易证PF∥GH;
(3)利用三角形外角定理、三角形内角和定理求得![]() ;然后由邻补角的定义、角平分线的定义推知
;然后由邻补角的定义、角平分线的定义推知![]() ;最后根据图形中的角与角间的和差关系求得∠HPQ=45°.
;最后根据图形中的角与角间的和差关系求得∠HPQ=45°.
(1)AB∥CD,
理由如下:
∵∠1与∠2互补,
∴∠1+∠2=180°,
又∵∠1=∠AEF,∠2=∠CFE,
∴∠AEF+∠CFE=180°,
∴AB∥CD;
(2)由(1)知,AB∥CD,∴∠BEF+∠EFD=180°.
又∵∠BEF与∠EFD的角平分线交于点P,
∴![]()
∴∠EPF=90°,即EG⊥PF.
∵GH⊥EG,
∴PF∥GH;
(3)∵∠PHK=∠HPK,
∴∠PKG=2∠HPK.
又∵GH⊥EG,
∴∠KPG=90°﹣∠PKG=90°﹣2∠HPK,
∴∠EPK=180°﹣∠KPG=90°+2∠HPK.
∵PQ平分∠EPK,
∴![]() ,
,
∴∠HPQ=∠QPK﹣∠HPK=45°.
答:∠HPQ的度数为45°.

【题目】某校决定在4月7日开展“世界无烟日”宣传活动,活动有A社区板报、B集会演讲、C喇叭广播、D发宣传画四种宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了两种不完整的统计图表:
选项 | 方式 | 百分比 |
A | 社区板报 | 35% |
B | 集会演讲 | m |
C | 喇叭广播 | 25% |
D | 发宣传画 | 10% |
请结合统计图表,回答下列问题:
(1)本次抽查的学生共人,m= , 并将条形统计图补充完整;
(2)若该校学生有1500人,请你估计该校喜欢“集会演讲”这项宣传方式的学生约有多少人?
(3)学校采用抽签方式让每班在A、B、C、D四种宣传方式在随机抽取两种进行展示,请用树状图或列表法求某班所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率.