题目内容
【题目】如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB,AC于E,F,已知EF∥BC.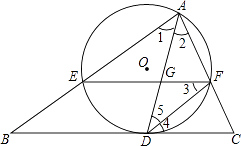
(1)求证:BC是⊙O的切线;
(2)若已知AE=9,CF=4,求DE长;
(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.
【答案】
(1)证明:连接OD, 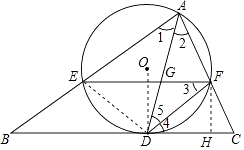
∵AD是△ABC的角平分线,
∴∠1=∠2,
∴ ![]() =
= ![]() ,
,
∴OD⊥EF,
∵EF∥BC,
∴OD⊥BC,
∴BC是⊙O的切线
(2)解:连接DE,
∵ ![]() =
= ![]() ,
,
∴DE=DF,
∵EF∥BC,
∴∠3=∠4,
∵∠1=∠3,
∴∠1=∠4,
∵∠DFC=∠AED,
∴△AED∽△DFC,
∴ ![]() ,即
,即 ![]() ,
,
∴DE2=36,
∴DE=6
(3)解:过F作FH⊥BC于H,
∵∠BAC=60°,
∴∠1=∠2=∠3=∠4=30°,
∴FH= ![]() DF=
DF= ![]() =3,DH=3
=3,DH=3 ![]() ,
,
∴CH= ![]() =
= ![]() ,
,
∵EF∥BC,
∴∠C=∠AFE,
∴tan∠AFE=tan∠C= ![]() =
= ![]() ;
;
∵∠4=∠2.∠C=∠C,
∴△ADC∽△DFC,
∴ ![]() ,
,
∵∠5=∠5,∠3=∠2,
∴△ADF∽△FDG,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴DG= ![]() .
.
【解析】(1)连半径,证垂直。连接OD,由AD是△ABC的角平分线。得出圆周角相等,继而得弧相等,根据垂径定理得出OD⊥EF,再根据EF∥BC,得到OD⊥BC,即可得证。
(2)先证明DE=DF,再证明△AED∽△DFC,根据相似三角形的性质得对应边成比例,即可求出DE的长。
(3)抓住已知∠BAC=60°,既可以证得∠4=30°,由此添加辅助线过F作FH⊥BC于H,Rt△DFH和Rt△FHC中就可以求出线段FH、DH、CH的长,根据平行得角相等,即可求出an∠AFE的值,再证明△ADC∽△DFC和△ADF∽△FDG,找到中间比,继而就可以求出DG的长。
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对切线的判定定理的理解,了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案