题目内容
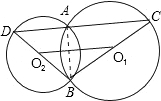
如图,⊙O1与⊙O2相交于A、B两点,BO2切⊙O1于点B,BO2的延长线交⊙O2于点D,DA的延长线 交⊙O1于点C.
交⊙O1于点C.
(1)证明:DB⊥BC;
(2)如果AC=3AD,求∠C的度数;
(3)在(2)的情况下,若⊙O2的半径为6,求四边形O1O2CD的面积.
 交⊙O1于点C.
交⊙O1于点C.(1)证明:DB⊥BC;
(2)如果AC=3AD,求∠C的度数;
(3)在(2)的情况下,若⊙O2的半径为6,求四边形O1O2CD的面积.
(1)证明:连接AB,∵BC是⊙O1的直径,
∴BA⊥CD,(1分)
所以BD是⊙O2的直径.(2分)
又∵BD是⊙O1的切线,所以DB⊥BC.(3分)
(2)∵AC=3AD;
∴AD=
DC,
∵BD2=DA•DC=
DC2,(5分)
∴BD=
DC,(6分)
∴∠C=30°.(7分)
(3)设⊙O1、⊙O2的半径分别为r1、r2.
∵⊙O2的半径为6,
∴AB=6
,
∴r1=6
,(9分)
∴AC=18,
∴AD=6,
∵O1O2是△BCD的中位线,O1O2=
DC=12,(11分)
AB=3
,
∴S梯形O1O2CD=
(24+12)×3
=54
.(12分)
∴BA⊥CD,(1分)
所以BD是⊙O2的直径.(2分)
又∵BD是⊙O1的切线,所以DB⊥BC.(3分)
(2)∵AC=3AD;
∴AD=
| 1 |
| 4 |
∵BD2=DA•DC=
| 1 |
| 4 |
∴BD=
| 1 |
| 2 |
∴∠C=30°.(7分)
(3)设⊙O1、⊙O2的半径分别为r1、r2.
∵⊙O2的半径为6,
∴AB=6
| 3 |
∴r1=6
| 3 |
∴AC=18,
∴AD=6,
∵O1O2是△BCD的中位线,O1O2=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴S梯形O1O2CD=
| 1 |
| 2 |
| 3 |
| 3 |


练习册系列答案
相关题目

 过C作⊙A的切线交x轴于点B.
过C作⊙A的切线交x轴于点B.

 交过A、B两点的切线于D、C,连接OC、BP,过点O作OM
交过A、B两点的切线于D、C,连接OC、BP,过点O作OM

