题目内容
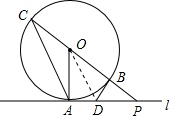
如图，直线l切⊙O于点A，点P为直线l上一点，直线PO交⊙O于点C、B，点D在线段AP上，连接DB，且AD=DB．
（1）求证：DB为⊙O的切线．
（2）若AD=1，PB=BO，求弦AC的长．
（1）求证：DB为⊙O的切线．
（2）若AD=1，PB=BO，求弦AC的长．
（1）证明：连接OD；
∵PA为⊙O切线，
∴∠OAD=90°；
在△OAD和△OBD中，
，
∴△OAD≌△OBD，
∴∠OBD=∠OAD=90°，
∴OB⊥BD
∴DB为⊙O的切线
（2）在Rt△OAP中；
∵PB=OB=OA，
∴OP=2OA，
∴∠OPA=30°，
∴∠POA=60°=2∠C，
∴PD=2BD=2DA=2，
∴∠OPA=∠C=30°，
∴AC=AP=3．
∵PA为⊙O切线，
∴∠OAD=90°；
在△OAD和△OBD中，
|
∴△OAD≌△OBD，
∴∠OBD=∠OAD=90°，
∴OB⊥BD
∴DB为⊙O的切线
（2）在Rt△OAP中；
∵PB=OB=OA，
∴OP=2OA，
∴∠OPA=30°，
∴∠POA=60°=2∠C，
∴PD=2BD=2DA=2，
∴∠OPA=∠C=30°，
∴AC=AP=3．
练习册系列答案
相关题目
点D，且∠D=∠BAC．
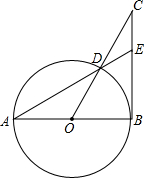
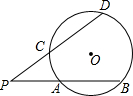
交⊙O1于点C．
