Question

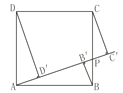
【题目】如图，正方形ABCD的边长为1，点P为BC上任意一点（可与点B或C重合），分别过B、C、D作射线AP的垂线，垂足分别是B′、C′、D′，则BB′＋CC′＋DD′的最小值是（　　）

A. 1 B. C. D.

Answer 1

【答案】B

【解析】试题解析：连接AC，DP．

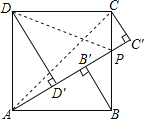
∵四边形ABCD是正方形，正方形ABCD的边长为1，

∴AB=CD，S正方形ABCD=1，

∵S△ADP=S正方形ABCD=，S△ABP+S△ACP=S△ABC=S正方形ABCD=，

∴S△ADP+S△ABP+S△ACP=1，

∴APBB′+APCC′+APDD′=AP（BB′+CC′+DD′）=1，

则BB′+CC′+DD′=，

∵1≤AP≤，

∴当P与C重合时，有最小值．

故选B.