Question

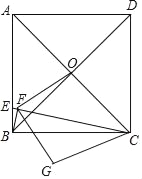
【题目】如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE＝∠B.

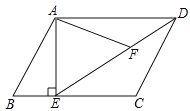
(1)求证：∠DFA＝∠ECD；

(2)△ADF与△DEC相似吗？为什么？

(3)若AB＝4，AD＝3，AE＝3，求AF的长．

Answer 1

【答案】（1）详见解析；（2）△ADF∽△DEC，理由详见解析；（3）AF＝2.

【解析】

（1）因为∠AFE＝∠B，平行四边形的邻角互补可得：∠B+∠ECD=180°；，等角的补角相等，所以∠AFE的领补角∠DFA=∠ECD；

（2）根据两角对应相等的两个三角形相似证明；

(3) 由平行四边形ABCD中，过点A作AE⊥BC，AB=4，AD=3，AE=3，由勾股定理可求得DE的长，又由∠AFE=∠B，易证得△ADF∽△DEC，然后由相似三角形的对应边成比例，即可求得答案．

(1)证明：∵∠AFE∠DFA＝180°，又∵四边形ABCD为平行四边形，∴∠B+∠ECD＝180°，又∵∠B＝∠AFE，∴∠DFA＝∠ECD.　

(2)解：△ADF∽△DEC.∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∴∠ADF＝∠CED，∠B＋∠C＝180°，∵∠AFE＋∠AFD＝180°，∠AFE＝∠B，∴∠AFD＝∠C，∴△ADF∽△DEC.　

(3)解：∵四边形ABCD是平行四边形，∴AD∥BC，CD＝AB＝4，又∵AE⊥BC，∴AE⊥AD，在Rt△ADE中，DE＝ ＝=6 ，∵△ADF∽△DEC，∴＝ ，∴＝，AF＝2 .