题目内容
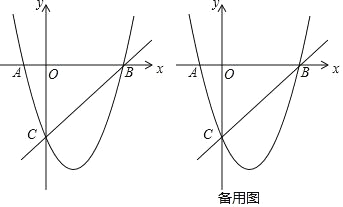
【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y=![]() x2+bx+c经过B点,且顶点在直线y=
x2+bx+c经过B点,且顶点在直线y=![]() 上.
上.
(1)求抛物线对应的函数关系式;
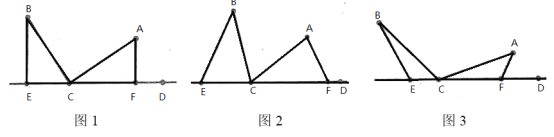
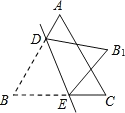
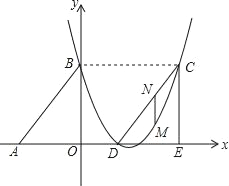
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由.
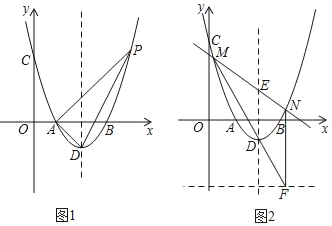
(3)在(2)的条件下,若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为s,求s与t之间的函数关系式,写出自变量t的取值范围,并求s取大值时,点M的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x+4;(2)点C和点D在所求抛物线上;(3)s=﹣
x+4;(2)点C和点D在所求抛物线上;(3)s=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,当s最大时,此时点M的坐标为(
,当s最大时,此时点M的坐标为(![]() ,
,![]() ).
).
【解析】
(1)已知了抛物线上A、B点的坐标以及抛物线的对称轴方程,可用待定系数法求出抛物线的解析式.
(2)首先求出AB的长,将A、B的坐标向右平移AB个单位,即可得出C、D的坐标,再代入抛物线的解析式中进行验证即可.
(3)根据C、D的坐标,易求得直线CD的解析式;那么线段MN的长实际是直线BC与抛物线的函数值的差,可将x=t代入两个函数的解析式中,得出的两函数值的差即为l的表达式,由此可求出l、t的函数关系式,根据所得函数的性质即可求出l取最大值时,点M的坐标.
(1)∵y=![]() x2+bx+c的顶点在直线x=
x2+bx+c的顶点在直线x=![]() 上,
上,
∴可设所求抛物线对应的函数关系式为y=![]() (x﹣
(x﹣![]() )2+m,
)2+m,
∵点B(0,4)在此抛物线上,
∴4=![]() (0﹣
(0﹣![]() )2+m,
)2+m,
∴m=﹣![]() ,
,
∴所求函数关系式为:y=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() =
=![]() x2﹣
x2﹣![]() x+4;
x+4;
(2)在Rt△ABO中,OA=3,OB=4,
∴AB=![]() =5.
=5.
∵四边形ABCD是菱形,
∴BC=CD=DA=AB=5,
∵A、B两点的坐标分别为(﹣3,0))、(0,4),
∴C、D两点的坐标分别是(5,4)、(2,0);
当x=5时,y=![]() ×52﹣
×52﹣![]() ×5+4=4,
×5+4=4,
当x=2时,y=![]() ×22﹣
×22﹣![]() ×2+4=0,
×2+4=0,
∴点C和点D在所求抛物线上;
(3)设直线CD对应的函数关系式为y=kx+n,
则![]() ,
,
解得: ;
;
∴y=![]() x﹣
x﹣![]() .
.
∵MN∥y轴,M点的横坐标为t,
∴N点的横坐标也为t;
则yM=![]() t2﹣
t2﹣![]() t+4,yN=
t+4,yN=![]() t﹣
t﹣![]() ,
,
∴s=yN﹣yM=(![]() t﹣
t﹣![]() )﹣(
)﹣(![]() t2﹣
t2﹣![]() t+4)
t+4)
=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当t=![]() 时,s最大=
时,s最大=![]() ,此时yM=
,此时yM=![]() ×(
×(![]() )2﹣
)2﹣![]() ×
×![]() +4=
+4=![]() .
.
此时点M的坐标为(![]() ,
,![]() ).
).