题目内容
【题目】阅读材料，解答问题.
例：用图象法解一元二次不等式：
解：设
，则
是
的二次函数.∵
，
∴抛物线开口向上.
又∵当
时，
，解得
，
.
∴由此得抛物线的大致图象如图所示.
观察函数图象可知：当
或
时，
.
∴的解集是：或.
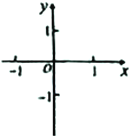
（1）观察图象，直接写出一元二次不等式：
的解集是______；
（2）仿照材料、用图象法解一元二次不等式：
.
【答案】（1）
；（2）
或
【解析】
观察图象即可得答案；（2）设
，可求出二次函数图象与x轴的交点的横坐标，即可得抛物线的大致图象，观察图象即可得
的解集.
（1）观察图象可知：时，y<0，
∴
的解集是，
故答案为：
（2）设，则
是
的二次函数，
∵
，
∴抛物线开口向上.
又∵当
时，
，解得
，
.
∴由此得抛物线的大致图象如图所示.
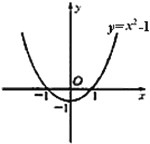
观察函数图象可知：当或时，
.
∴的解集是：或.
练习册系列答案
相关题目
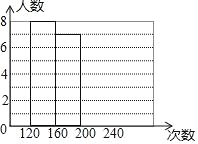
【题目】某体育老师随机抽取了九年级甲、乙两班部分学生进行一分钟跳绳的测试，并对成绩进行统计分析，绘制了频数分布表和统计图，请你根据图表中的信息完成下列问题：
分组 | 频数 | 频率 |
第一组(0≤x<120) | 3 | 0.15 |
第二组(120≤x<160) | 8 | a |
第三组(160≤x<200) | 7 | 0.35 |
第四组(200≤x<240) | b | 0.1 |
(1)频数分布表中a＝____，b＝_____，并将统计图补充完整；
(2)如果该校九年级共有学生360人，估计跳绳能够一分钟完成160或160次以上的学生有多少人？
(3)已知第一组中有两个甲班学生，第四组中只有一个甲班学生，老师随机从这两个组中各选一名学生谈测试体会，则所选两人正好都是甲班学生的概率是多少？
