题目内容
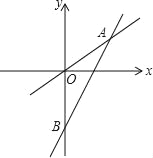
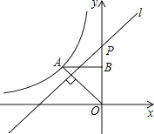
【题目】如图,反比例函数y=![]() (x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B'在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B'在此反比例函数的图象上,则t的值是( )
A. 1+![]() B. 4+
B. 4+![]() C. 4
C. 4![]() D. -1+
D. -1+![]()
【答案】A
【解析】
根据反比例函数图象上点的坐标特征由A点坐标为(-2,2)得到k=-4,即反比例函数解析式为y=-![]() ,且OB=AB=2,则可判断△OAB为等腰直角三角形,所以∠AOB=45°,再利用PQ⊥OA可得到∠OPQ=45°,然后轴对称的性质得PB=PB′,BB′⊥PQ,所以∠BPQ=∠B′PQ=45°,于是得到B′P⊥y轴,则点B的坐标可表示为(-
,且OB=AB=2,则可判断△OAB为等腰直角三角形,所以∠AOB=45°,再利用PQ⊥OA可得到∠OPQ=45°,然后轴对称的性质得PB=PB′,BB′⊥PQ,所以∠BPQ=∠B′PQ=45°,于是得到B′P⊥y轴,则点B的坐标可表示为(-![]() ,t),于是利用PB=PB′得t-2=|-
,t),于是利用PB=PB′得t-2=|-![]() |=
|=![]() ,然后解方程可得到满足条件的t的值.
,然后解方程可得到满足条件的t的值.
如图,
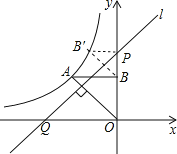
∵点A坐标为(-2,2),
∴k=-2×2=-4,
∴反比例函数解析式为y=-![]() ,
,
∵OB=AB=2,
∴△OAB为等腰直角三角形,
∴∠AOB=45°,
∵PQ⊥OA,
∴∠OPQ=45°,
∵点B和点B′关于直线l对称,
∴PB=PB′,BB′⊥PQ,
∴∠B′PQ=∠OPQ=45°,∠B′PB=90°,
∴B′P⊥y轴,
∴点B′的坐标为(-![]() ,t),
,t),
∵PB=PB′,
∴t-2=|-![]() |=
|=![]() ,
,
整理得t2-2t-4=0,解得t1=![]() ,t2=1-
,t2=1-![]() (不符合题意,舍去),
(不符合题意,舍去),
∴t的值为![]() .
.
故选A.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去……
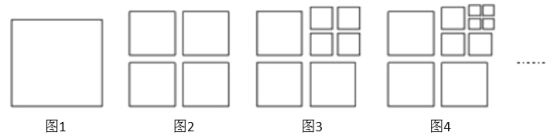
(1)根据图中的规律补全下表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
| n |
正方形个数 | 1 | 4 | 7 | 10 |
|
(2)求第几幅图形中有2020个正方形?