题目内容
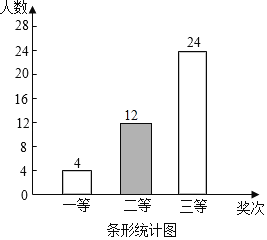
【题目】2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求本次比赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
【答案】(1)40,补图详见解析;(2)108°;(3)![]() .
.
【解析】
(1)由一等奖人数及其所占百分比可得总人数,总人数减去一等奖、三等奖人数求出二等奖人数即可补全图形;
(2)用360°乘以二等奖人数所占百分比可得答案;
(3)画出树状图,由概率公式即可解决问题.
解:(1)本次比赛获奖的总人数为4÷10%=40(人),
二等奖人数为40﹣(4+24)=12(人),
补全条形图如下:
(2)扇形统计图中“二等奖”所对应扇形的圆心角度数为360°×![]() =108°;
=108°;
(3)树状图如图所示,

∵从四人中随机抽取两人有12种可能,恰好是甲和乙的有2种可能,
∴抽取两人恰好是甲和乙的概率是![]() =
=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目