题目内容
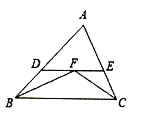
【题目】如图,△ABC∽△DEC,CA=CB,且点E在AB的延长线上.
(1)求证:AE=BD;
(2)求证:△BOE∽△COD;
(3)已知CD=10,BE=5,OD=6,求OC的长.

【答案】(1)详见解析;(2)详见解析;(3)CO=7.
【解析】
(1)利用相似三角形的性质:对应边的比值相等可证明CE=CD,再根据全等三角形的判定方法可证明△ACE≌△CBD,进而证明AE=BD;
(2)利用有两对角相等的两三角形相似即可证明:△BOE∽△COD.
(3)根据相似三角形的性质解答即可.
证明:(1)∵△ABC∽△DEC,CA=CB,
∴![]()
∴CE=CD,∠ACB=∠ECD,
∴∠ACB+∠BCE=∠ECD+∠BCE,
∴∠ACE=∠BCD,
在△ACE和△BCD中, ,
,
∴△ACE≌△BCD(SAS),
∴AE=BD;
(2)∵△ACE≌△BCD.
∴∠AEC=∠BDC,
∵∠DOC=∠EOB,
∴△COD∽△BOE,
(3)∵△BOE∽△COD.
∴![]() =
=![]() ,
,
∵CD=10,BE=5, OD=6,
∴![]() =
=![]()
∴OE=3
∴CO=CE﹣OE=CD﹣OE=10﹣3=7.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目